Sur ce thème
Méthode de Tukey pour un modèle à effets mixtes

Pour plus d'informations sur le calcul des moyennes ajustées et de l'erreur type de la différence, reportez-vous à la rubrique Méthodes et formules pour les moyennes ajustées dans la fonction Ajuster le modèle à effets mixtes.
Remarque
Les calculs de la statistique de test, de la valeur de p ajustée, du niveau de confiance individuel et du tableau d'informations de groupement correspondent aux calculs des modèles linéaires généraux. Pour plus d'informations, reportez-vous à la rubrique Méthodes et formules pour les comparaisons des modèles linéaires généraux.
Valeur critique

| Terme | Description |
|---|---|
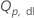 | valeur critique supérieure 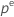 quantile de la loi T de l'étendue studentisée avec dl degrés de liberté quantile de la loi T de l'étendue studentisée avec dl degrés de liberté |
 | probabilité simultanée de faire une erreur de 1ère espèce |
| m | nombre de niveaux dans le terme |
| dl | degrés de liberté |
Les degrés de liberté varient selon que la comparaison concerne un terme à effets fixes ou un terme aléatoire.
Degrés de liberté (dl)
Pour un terme à effets fixes, les degrés de liberté (dl) sont les mêmes que pour le test du terme à effets fixes correspondant. Pour un terme aléatoire, les degrés de liberté utilisent la méthode d'approximation de Satterthwaite.
Pour plus d'informations sur le calcul des degrés de liberté, reportez-vous à la rubrique Méthodes et formules pour les tests des effets fixes dans la fonction Ajuster le modèle à effets mixtes.
Méthode de Fisher pour les comparaisons deux à deux dans un modèle à effets mixtes

Pour plus d'informations sur le calcul des moyennes ajustées et de l'erreur type de la différence, reportez-vous à la rubrique Méthodes et formules pour les moyennes ajustées dans la fonction Ajuster le modèle à effets mixtes.
Remarque
Les calculs de la statistique de test, de la valeur de p ajustée, du niveau de confiance individuel et du tableau d'informations de groupement correspondent aux calculs des modèles linéaires généraux. Pour plus d'informations, reportez-vous à la rubrique Méthodes et formules pour les comparaisons des modèles linéaires généraux.
Valeur critique
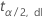
| Terme | Description |
|---|---|
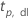 | percentile 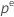 supérieur de la loi T de Student avec dl degrés de liberté supérieur de la loi T de Student avec dl degrés de liberté |
| α | probabilité individuelle de faire une erreur de 1ère espèce |
| dl | degrés de liberté |
Les degrés de liberté varient selon que la comparaison concerne un terme à effets fixes ou un terme aléatoire.
Degrés de liberté (dl)
Pour un terme à effets fixes, les degrés de liberté (dl) sont les mêmes que pour le test du terme à effets fixes correspondant. Pour un terme aléatoire, les degrés de liberté utilisent la méthode d'approximation de Satterthwaite.
Pour plus d'informations sur le calcul des degrés de liberté, reportez-vous à la rubrique Méthodes et formules pour les tests des effets fixes dans la fonction Ajuster le modèle à effets mixtes.
Méthode de Bonferroni pour les comparaisons deux à deux dans un modèle à effets mixtes

Pour plus d'informations sur le calcul des moyennes ajustées et de l'erreur type de la différence, reportez-vous à la rubrique Méthodes et formules pour les moyennes ajustées dans la fonction Ajuster le modèle à effets mixtes.
Remarque
Les calculs de la statistique de test, de la valeur de p ajustée, du niveau de confiance individuel et du tableau d'informations de groupement correspondent aux calculs des modèles linéaires généraux. Pour plus d'informations, reportez-vous à la rubrique Méthodes et formules pour les comparaisons des modèles linéaires généraux.
Valeur critique

| Terme | Description |
|---|---|
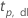 | percentile 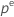 supérieur de la loi T de Student avec dl degrés de liberté supérieur de la loi T de Student avec dl degrés de liberté |
| α | probabilité simultanée de faire une erreur de 1ère espèce |
| c |  |
| k | nombre de niveaux du terme à effets fixes ou du terme aléatoire |
| dl | degrés de liberté |
Les degrés de liberté varient selon que la comparaison concerne un terme à effets fixes ou un terme aléatoire.
Degrés de liberté (dl)
Pour un terme à effets fixes, les degrés de liberté (dl) sont les mêmes que pour le test du terme à effets fixes correspondant. Pour un terme aléatoire, les degrés de liberté utilisent la méthode d'approximation de Satterthwaite.
Pour plus d'informations sur le calcul des degrés de liberté, reportez-vous à la rubrique Méthodes et formules pour les tests des effets fixes dans la fonction Ajuster le modèle à effets mixtes.
Méthode de Sidak pour les comparaisons deux à deux dans un modèle à effets mixtes

Pour plus d'informations sur le calcul des moyennes ajustées et de l'erreur type de la différence, reportez-vous à la rubrique Méthodes et formules pour les moyennes ajustées dans la fonction Ajuster le modèle à effets mixtes.
Remarque
Les calculs de la statistique de test, de la valeur de p ajustée, du niveau de confiance individuel et du tableau d'informations de groupement correspondent aux calculs des modèles linéaires généraux. Pour plus d'informations, reportez-vous à la rubrique Méthodes et formules pour les comparaisons des modèles linéaires généraux.
Valeur critique
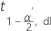
| Terme | Description |
|---|---|
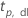 | percentile 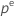 supérieur de la loi T de Student avec dl degrés de liberté supérieur de la loi T de Student avec dl degrés de liberté |
 | 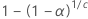 |
| α | probabilité simultanée de faire une erreur de 1ère espèce |
| c |  |
| k | nombre de niveaux du terme à effets fixes ou du terme aléatoire |
| dl | degrés de liberté |
Les degrés de liberté varient selon que la comparaison concerne un terme à effets fixes ou un terme aléatoire.
Degrés de liberté (dl)
Pour un terme à effets fixes, les degrés de liberté (dl) sont les mêmes que pour le test du terme à effets fixes correspondant. Pour un terme aléatoire, les degrés de liberté utilisent la méthode d'approximation de Satterthwaite.
Pour plus d'informations sur le calcul des degrés de liberté, reportez-vous à la rubrique Méthodes et formules pour les tests des effets fixes dans la fonction Ajuster le modèle à effets mixtes.
