Sur ce thème
Tableau d'informations de groupement pour comparaisons deux à deux multiples
Minitab utilise les résultats de l'intervalle de confiance pour la différence entre deux moyennes de niveau afin d'obtenir des informations de groupement. Les informations de groupement se trouvent dans une matrice. Supposons qu'un terme dispose de k niveaux, la dimension maximale de la matrice est k x k. Si tous les niveaux sont dans un groupe, la dimension est k x 1, et la lettre "A" est affectée pour tous les niveaux de facteurs. Si tous les niveaux sont dans des groupes différents, la dimension est k x k avec des lettres sur la diagonale uniquement.
- Triez toutes les moyennes des moindres carrés à différents niveaux d'un terme dans l'ordre décroissant, noté 1, 2, ..., k.
- Définissez une matrice k x k avec la valeur 0 dans chaque cellule où k = nombre de niveaux de facteurs.
- Pour la colonne j, où j = 1, ... , Minitab effectue les opérations suivantes :
- Vérifie les intervalles de confiance de la moyenne j – moyenne r, où r = j + 1, ... , k. Si l'intervalle pour r contient la valeur 0, Minitab définit la re ligne et la je cellule de colonne, j) sur la valeur 1.
- Définit la cellule (j, j) sur 1 si au moins une cellule de la colonne j contient la valeur 1.
- Calcule la somme des lignes de la colonne 1 à la colonne j pour la ligne I = j + 1, ... , k. Si la valeur minimale (somme de toutes les lignes) >= 1, la boucle doit être interrompue. Sinon, augmentez la valeur de j de 1 et reportez-vous à l'étape a.
- Pour chaque ligne i, Minitab vérifie la somme de la valeur de toutes les colonnes pour la ligne ≥ 1. Si la somme est égale à zéro, définissez la cellule de la ligne i et de la colonne j sur 1, où la colonne j est la première colonne dans la matrice contenant des valeurs égales à 0. Cette procédure génère une matrice avec des valeurs égales à 1 et 0. Le nombre total de groupes correspond au nombre de colonnes qui ne contiennent pas la valeur zéro.
- Minitab fait correspondre des lettres à des colonnes (par exemple, A pour Colonne 1, B pour Colonne 2, etc.) et affecte aux cellules contenant la valeur 1 la lettre nécessaire.
Tableau d'informations de groupement pour comparaisons multiples avec un contrôle
Minitab utilise les résultats de l'intervalle de confiance pour la différence entre chaque moyenne de niveau et le niveau de contrôle afin d'obtenir des informations de groupement. Les informations de groupement se trouvent dans une matrice à une colonne.
Minitab affecte la lettre "A" au niveau de contrôle.
Si un intervalle contient le chiffre 0, la moyenne de niveau se trouve dans le même groupe que le niveau de contrôle. Minitab affecte la lettre "A" à la moyenne de niveau.
Si un intervalle ne contient pas la valeur zéro, la lettre n'est pas affectée.
Méthode de Tukey
Formule
La méthode de Tukey est disponible pour toutes les comparaisons deux à deux. La formule pour les intervalles de confiance est la suivante :

La formule pour la statistique de test est la suivante :
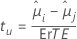
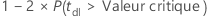
Pour plus d'informations sur le calcul de la valeur de p ajustée, reportez-vous aux références ci-dessous.
Pour connaître le taux d'erreur individuel à partir du taux d'erreur simultané, utilisez la formule suivante :
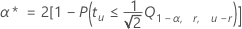
Notation
| Terme | Description |
|---|---|
 | moyenne issue des moindres carrés pour le/la ie niveau de facteur ou combinaison de niveaux de facteurs |
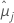 | moyenne issue des moindres carrés pour le/la je niveau de facteur ou combinaison de niveaux de facteurs |
| r | nombre de moyennes |
| Q1 − α, r, u | percentile 1 − α de la loi de l’étendue studentisée pour r moyennes à comparer avec u degrés de liberté |
| u | degrés de liberté pour l'erreur dans le modèle |
| ErTE | erreur type de la différence estimée entre les moyennes issues des moindres carrés |
| α | probabilité simultanée de faire une erreur de 1ère espèce, en fonction de la loi de l'étendue studentisée |
| α* | probabilité individuelle de faire une erreur de 1ère espèce, en fonction de la loi t pour une comparaison |
Références
1 Braun, H. I., editor (1994). The collected works of John W. Tukey: Volume VIII Multiple comparisons 1948-1983. New York: Chapman and Hall.
2 J.C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
Méthode de Fisher
Formule
Minitab propose différentes méthodes d'intervalles de confiance pour la comparaison des moyennes de traitements. Pour la méthode de Fisher, les bornes de l'intervalle de confiance et les valeurs de p sont les mêmes, qu'il s'agisse de comparaisons deux à deux ou avec un contrôle. La méthode de Fisher utilise le niveau de confiance individuel. La formule pour les intervalles de confiance est la suivante :
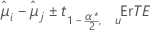
La formule pour la statistique de test est la suivante :
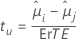
Valeur de p = 2*P{ T u > tu}
Pour connaître le niveau de confiance simultané à partir du taux d'erreur individuel, utilisez la formule suivante :

Notation
| Terme | Description |
|---|---|
 | moyenne issue des moindres carrés pour le/la ie niveau de facteur ou combinaison de niveaux de facteurs |
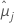 | moyenne issue des moindres carrés pour le/la je niveau de facteur ou combinaison de niveaux de facteurs |
| t1-α*/2, u | percentile α*/2 supérieur de la loi T de Student avec u degrés de liberté |
| Tu | Variable aléatoire avec une loi T ayant u degrés de liberté pour l'erreur |
| T | variable aléatoire avec une loi de l’étendue studentisée |
| α | probabilité simultanée de faire une erreur de 1ère espèce |
| α* | probabilité individuelle de faire une erreur de 1ère espèce |
| u | degrés de liberté pour l'erreur dans le modèle |
| ErTE | erreur type de la différence estimée entre les moyennes issues des moindres carrés |
Méthode de Bonferroni
Formule
Minitab propose différentes méthodes d'intervalles de confiance pour la comparaison des moyennes de traitements. La méthode de Bonferroni n'émet aucune hypothèse concernant la dépendance entre les comparaisons, il s'agit de la méthode la plus prudente. "Prudente" dans ce contexte signifie que le niveau de confiance réel est susceptible d'être supérieur au niveau de confiance affiché. La formule pour les intervalles de confiance est la suivante :

La formule pour la statistique de test est la suivante :
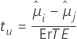
Notation
| Terme | Description |
|---|---|
 | moyenne issue des moindres carrés pour le/la ie niveau de facteur ou combinaison de niveaux de facteurs |
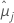 | moyenne issue des moindres carrés pour le/la je niveau de facteur ou combinaison de niveaux de facteurs |
| t1-α*/2, u | percentile α' /2 supérieur de la loi T de Student avec u degrés de liberté |
| α | probabilité simultanée de faire une erreur de 1ère espèce |
| α' | α / c |
| c | nombre de comparaisons |
| u | degrés de liberté pour l'erreur dans le modèle |
| ErTE | erreur type de la différence estimée entre les moyennes issues des moindres carrés |
Le nombre de comparaisons varie selon qu'il s'agit de comparaisons deux à deux ou avec un contrôle. Soit k le nombre de moyennes en cours de comparaison. Le nombre de comparaisons figure dans le tableau ci-dessous.
| Deux à deux | k (k – 1) / 2 |
| Avec un contrôle | k – 1 |
Méthode de Sidak
Formule
Minitab propose différentes méthodes d'intervalles de confiance pour la comparaison des moyennes de traitements. La méthode de Sidak traite les comparaisons comme si elles étaient indépendantes, ce qui engendre une approximation conservatrice du taux d'erreur réel. La méthode de Sidak est légèrement plus puissante que celle de Bonferroni.
La formule pour les intervalles de confiance est la suivante :

La formule pour la statistique de test est la suivante :
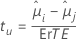
Valeur de p ajustée = 1 − (1 − p)c.
Notation
| Terme | Description |
|---|---|
 | moyenne issue des moindres carrés pour le/la ie niveau de facteur ou combinaison de niveaux de facteurs |
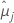 | moyenne issue des moindres carrés pour le/la je niveau de facteur ou combinaison de niveaux de facteurs |
| t1-α*/2, u | percentile α' /2 supérieur de la loi T de Student avec u degrés de liberté |
| α | probabilité simultanée de faire une erreur de 1ère espèce |
| α' | 1 – (1 – α ) 1/ k |
| u | degrés de liberté pour l'erreur dans le modèle |
| ErTE | erreur type de la différence estimée entre les moyennes issues des moindres carrés |
| p | Valeur de p non ajustée provenant de la loi t pour une comparaison |
| c | nombre de comparaisons |
Le nombre de comparaisons varie selon qu'il s'agit de comparaisons deux à deux ou avec un contrôle. Soit k le nombre de combinaisons de facteurs. Le nombre de comparaisons figure dans le tableau ci-dessous.
| Deux à deux | k (k – 1) / 2 |
| Avec un contrôle | k – 1 |
Méthode de Dunnett
Formule
Minitab propose différentes méthodes d'intervalles de confiance pour la comparaison des moyennes de traitements. La méthode de Dunnett est disponible pour les comparaisons avec un contrôle. La formule pour les intervalles de confiance est la suivante :
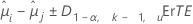
La formule pour la statistique de test est la suivante :
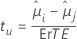
La valeur de p ajustée provient de l'intégration de la loi proposée par Dunnett pour la statistique de test. Pour plus d'informations, reportez-vous aux références ci-dessous.
Notation
| Terme | Description |
|---|---|
 | moyenne issue des moindres carrés pour le/la ie niveau de facteur ou combinaison de niveaux de facteurs |
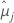 | moyenne issue des moindres carrés pour le/la je niveau de facteur ou combinaison de niveaux de facteurs |
| D1-α, k-1, u | percentile α supérieur de la loi proposée par Dunnett avec k − 1 comparaisons et u degrés de liberté |
| α | probabilité simultanée de faire une erreur de 1ère espèce |
| k | nombre de moyennes à comparer |
| u | degrés de liberté pour l'erreur dans le modèle |
| ErTE | erreur type de la différence estimée entre les moyennes issues des moindres carrés |
Références
1 Dunnett, C. W. (January 01, 1955). A multiple comparison procedure for comparing several treatments with a control. Journal of the American Statistical Association, 50, 1096-1121.
2 J.C. Hsu (1996). Multiple Comparisons: Theory and methods. Chapman & Hall.
