Sur ce thème
N
L'effectif de l'échantillon (N) est le nombre total d'observations dans chaque groupe.
Interprétation
L'effectif de l'échantillon a une influence sur l'intervalle de confiance et la puissance du test.
En général, plus l'échantillon est grand, plus l'intervalle de confiance est étroit. En outre, un effectif d'échantillon plus grand donne au test plus de puissance pour détecter une différence.
Moyenne
Moyenne des observations dans chaque groupe. La moyenne décrit chaque groupe avec une seule valeur, qui représente le centre des données. Il s'agit de la somme de toutes les observations avec un groupe divisée par le nombre d'observations dans ce groupe.
Interprétation
La moyenne de chaque échantillon fournit une estimation de la moyenne de chaque population. Les différences entre les moyennes d'échantillons correspondent aux estimations de la différence entre les moyennes de populations.
Puisque la différence entre les moyennes de groupes repose sur les données provenant d'un échantillon plutôt que sur l'ensemble de la population, vous ne pouvez pas être sûr qu'elle est égale à la différence de population. Pour mieux évaluer la différence de la population, vous pouvez utiliser l'intervalle de confiance.
Groupement
Utilisez le tableau d'informations de groupement pour déterminer rapidement si la différence moyenne entre toute paire de groupes est statistiquement significative.
La colonne Groupement contient des lettres qui regroupent les niveaux de facteurs. La différence moyenne des groupes qui ne partagent pas de lettre est statistiquement significative.
Si le tableau indique des différences statistiquement significatives, utilisez les intervalles de confiance des différences afin de déterminer si elles sont significatives sur le plan concret.
Vous pouvez effectuer une analyse par comparaison multiple de termes aléatoires pour déterminer les niveaux du terme significativement différents des autres niveaux. Par exemple, si vous étudiez l'efficacité d'un médicament sur une maladie particulière, le sujet représente généralement un facteur aléatoire significatif. Vous pouvez utiliser des comparaisons multiples pour déterminer si le médicament a eu des effets différents sur des sujets spécifiques (il a peut-être rendu l'un d'entre eux plus malade).
Interprétation
Informations de groupement avec la méthode de Tukey et un niveau de confiance de 95 %
| Peinture | N | Moyenne | Groupement | |
|---|---|---|---|---|
| Mélange4 | 6 | 18,07 | A | |
| Mélange1 | 6 | 14,73 | A | B |
| Mélange3 | 6 | 12,98 | A | B |
| Mélange2 | 6 | 8,57 | B | |
Dans ces résultats, le tableau montre que le groupe A contient les mélanges 1, 3 et 4, et que le groupe B contient les mélanges 1, 2 et 3. Les mélanges 1 et 3 sont dans les deux groupes. Les différences entre les moyennes qui partagent une lettre ne sont pas statistiquement significatives. Les mélanges 2 et 4 ne partagent pas de lettre, ce qui indique que la moyenne du mélange 4 est bien plus élevée que celle du mélange 2.
Tests individuels de Fisher pour les différences des moyennes
Utilisez les intervalles de confiance individuels pour identifier les différences statistiquement significatives entre les moyennes de groupes, afin de déterminer les étendues de valeurs probables pour les différences et afin de déterminer si les différences sont significatives sur le plan concret. Le tableau des tests individuels de Fisher affiche un ensemble d'intervalles de confiance pour la différence entre des paires de moyennes.
Le niveau de confiance individuel est le pourcentage d'occurrences, dans un même intervalle de confiance, de la différence réelle entre une paire de moyennes de groupes, si l'étude est répétée. Les intervalles de confiance individuels sont disponibles uniquement pour la méthode de Fisher. Toutes les autres méthodes de comparaison génèrent des intervalles de confiance simultanés.
Le contrôle du niveau de confiance individuel est peu fréquent, car il ne contrôle pas le niveau de confiance simultané, qui atteint souvent des niveaux inacceptables. Si vous ne le contrôlez pas, la probabilité qu'au moins un intervalle de confiance ne contienne pas la différence réelle augmente avec le nombre de comparaisons.
L'intervalle de confiance de la différence est composé des deux parties suivantes :
- Estimation ponctuelle
- L'estimation ponctuelle est la différence entre une paire de moyennes et est calculée à partir des données des échantillons. L'intervalle de confiance est centré sur cette valeur.
- Marge d'erreur
- La marge d'erreur définit la largeur de l'intervalle de confiance et est déterminée par la variabilité observée dans l'échantillon et le niveau de confiance. Pour calculer la limite supérieure de l'intervalle de confiance, la marge d'erreur est ajoutée à l'estimation ponctuelle. Pour calculer la limite inférieure de l'intervalle de confiance, la marge d'erreur est soustraite de l'estimation ponctuelle.
Interprétation
Utilisez les intervalles de confiance pour évaluer les différences entre les moyennes de groupes.
Tests individuels de Fisher pour les différences des moyennes
| Différence des niveaux | Différence des moyennes | Erreur type de la différence | IC à 95 % | Valeur de T | Valeur de p ajustée |
|---|---|---|---|---|---|
| Mélange2 - Mélange1 | -6,17 | 2,28 | (-10,92; -1,41) | -2,70 | 0,014 |
| Mélange3 - Mélange1 | -1,75 | 2,28 | (-6,51; 3,01) | -0,77 | 0,452 |
| Mélange4 - Mélange1 | 3,33 | 2,28 | (-1,42; 8,09) | 1,46 | 0,159 |
| Mélange3 - Mélange2 | 4,42 | 2,28 | (-0,34; 9,17) | 1,94 | 0,067 |
| Mélange4 - Mélange2 | 9,50 | 2,28 | (4,74; 14,26) | 4,17 | 0,000 |
| Mélange4 - Mélange3 | 5,08 | 2,28 | (0,33; 9,84) | 2,23 | 0,037 |
- L'intervalle de confiance pour la différence entre les moyennes des mélanges 4 et 2 s'étend de 4,74 à 14,26. Cette étendue ne comprend pas la valeur zéro, ce qui indique que la différence entre ces moyennes est statistiquement significative.
- L'intervalle de confiance pour la différence entre les moyennes des mélanges 2 et 1 s'étend de -10,92 à -1,41. Cette étendue ne comprend pas la valeur zéro, ce qui indique que la différence entre ces moyennes est statistiquement significative.
- L'intervalle de confiance pour la différence entre les moyennes des mélanges 4 et 3 s'étend de 0,33 à 9,84. Cette étendue ne comprend pas la valeur zéro, ce qui indique que la différence entre ces moyennes est statistiquement significative.
- Les intervalles de confiance pour toutes les paires de moyennes restantes comprennent tous la valeur zéro, ce qui indique que les différences ne sont pas statistiquement significatives.
- Le niveau de confiance individuel à 95 % indique que vous pouvez être sûr à 95 % que chaque intervalle de confiance individuel contient la différence réelle pour une comparaison spécifique. Toutefois, le niveau de confiance simultané indique que vous ne pouvez être sûr qu'à 80,83 % que tous les intervalles contiennent les différences réelles.
Différence des moyennes
Cette valeur représente la différence entre les moyennes d'échantillons de deux groupes.
Interprétation
Les différences entre les moyennes d'échantillons des groupes sont des estimations des différences entre les populations de ces groupes.
Puisque chaque différence repose sur les données provenant d'un échantillon plutôt que sur l'ensemble de la population, vous ne pouvez pas être sûr qu'elle est égale à la différence de population. Pour mieux comprendre les différences entre les moyennes de populations, utilisez les intervalles de confiance.
Erreur type de la différence
L'erreur type de la différence entre les moyennes (ErT de la différence) estime la variabilité de la différence entre les moyennes d'échantillons que vous obtiendriez si vous preniez des échantillons répétés des mêmes populations.
Interprétation
Utilisez l'erreur type de la différence entre les moyennes pour déterminer la précision avec laquelle les différences entre les moyennes d'échantillons estiment les différences entre les moyennes de populations. Une valeur d'erreur type plus faible indique une estimation plus précise.
Minitab utilise l'erreur type de la différence pour calculer les intervalles de confiance des différences entre les moyennes, c'est-à-dire une étendue de valeurs susceptible de contenir les différences de populations.
DL
Les degrés de liberté (DL) représentent la quantité d'informations dans vos données. Minitab utilise les degrés de liberté pour calculer le test t de la différence entre les moyennes. Minitab affiche uniquement les degrés de liberté si vous effectuez des comparaisons pour un modèle à effets mixtes.
IC simultané à 95 %
Utilisez les intervalles de confiance simultanés de la différence (IC à 95 %) pour identifier les différences moyennes qui sont statistiquement significatives, afin de déterminer les étendues de valeurs probables pour les différences et d'évaluer la signification concrète de ces différences. Le tableau présente un ensemble d'intervalles de confiance pour la différence entre des paires de moyennes. Les intervalles de confiance qui ne contiennent pas la valeur zéro indiquent une différence moyenne qui est statistiquement significative.
Le niveau de confiance simultané correspond au pourcentage d'occurrences, dans un ensemble d'intervalles de confiance, des différences réelles pour toutes les comparaisons de groupes si l'étude est répétée plusieurs fois.
Le contrôle du niveau de confiance simultané est particulièrement important lorsque vous réalisez plusieurs comparaisons. Si vous ne le contrôlez pas, la probabilité qu'au moins un intervalle de confiance ne contienne pas la différence réelle augmente avec le nombre de comparaisons.
Pour plus d'informations, reportez-vous à la rubrique Présentation des niveaux de confiance individuel et simultané dans les comparaisons multiples.
L'intervalle de confiance de la différence est composé des deux parties suivantes :
- Estimation ponctuelle
- L'estimation ponctuelle est la différence entre une paire de moyennes et est calculée à partir des données des échantillons. L'intervalle de confiance est centré sur cette valeur.
- Marge d'erreur
- La marge d'erreur définit la largeur de l'intervalle de confiance et est déterminée par la variabilité observée dans l'échantillon, l'effectif de l'échantillon et le niveau de confiance. Pour calculer la limite supérieure de l'intervalle de confiance, la marge d'erreur est ajoutée à l'estimation ponctuelle. Pour calculer la limite inférieure de l'intervalle de confiance, la marge d'erreur est soustraite de l'estimation ponctuelle. La marge s'étend à mesure que le nombre de comparaisons augmente afin de conserver le niveau simultané de confiance selon lequel tous les intervalles contiennent les différences de population réelles.
Vous pouvez effectuer une analyse par comparaison multiple de termes aléatoires pour déterminer les niveaux du terme significativement différents des autres niveaux. Par exemple, si vous étudiez l'efficacité d'un médicament sur une maladie particulière, le sujet représente généralement un facteur aléatoire significatif. Vous pouvez utiliser des comparaisons multiples pour déterminer si le médicament a eu des effets différents sur des sujets spécifiques (il a peut-être rendu l'un d'entre eux plus malade).
Interprétation
Utilisez les intervalles de confiance pour évaluer les différences entre les moyennes de groupes.
Tests de simultanéité de Tukey pour les différences des moyennes
| Différence des niveaux Sujet | Différence des moyennes | Erreur type de la différence | IC simultané à 95 % | Valeur de T | Valeur de p ajustée |
|---|---|---|---|---|---|
| 2 - 1 | 0,6567 | 0,0664 | (0,4768; 0,8366) | 9,89 | 0,000 |
| 3 - 1 | 0,9633 | 0,0708 | (0,7715; 1,1551) | 13,60 | 0,000 |
| 4 - 1 | 0,6900 | 0,0750 | (0,4870; 0,8930) | 9,20 | 0,000 |
| 3 - 2 | 0,3067 | 0,0632 | (0,1356; 0,4777) | 4,86 | 0,000 |
| 4 - 2 | 0,0333 | 0,0678 | (-0,1502; 0,2169) | 0,49 | 0,960 |
| 4 - 3 | -0,2733 | 0,0721 | (-0,4686; -0,0781) | -3,79 | 0,003 |
- L'intervalle de confiance pour la différence entre les moyennes des sujets 4 et 2 s'étend de -0,1502 à 0,2169. Cette étendue comprend la valeur zéro, ce qui indique que la différence n'est pas statistiquement significative.
- Les intervalles de confiance pour les paires de moyennes restantes ne comprennent pas la valeur zéro, ce qui indique que les différences sont statistiquement significatives.
- Le niveau de confiance simultané à 95 % indique que vous pouvez être sûr à 95 % que tous les intervalles de confiance contiennent les différences réelles.
- Le tableau indique que le niveau de confiance individuel est de 98,94 %. Ce résultat indique que vous pouvez être sûr à 98,94 % que chaque intervalle individuel contient la différence réelle dans une paire spécifique de moyennes de groupes.
- Le niveau de confiance individuel pour chaque comparaison génère collectivement le niveau de confiance simultané à 98,94 % pour les six comparaisons.
Valeur de t
La valeur de t est une statistique de test qui mesure le rapport entre la différence dans les moyennes et l'erreur type de la différence.
Interprétation
Vous pouvez utiliser la valeur de t pour déterminer si l'hypothèse nulle doit être rejetée, hypothèse qui stipule que la différence dans les moyennes est de 0. Toutefois, la valeur de p est plus couramment utilisée, car elle est plus facile à interpréter. Pour plus d'informations sur l'utilisation de la valeur critique, reportez-vous à Utiliser la valeur de t afin de déterminer si l'hypothèse nulle doit être rejetée.
Minitab utilise la valeur de t pour calculer la valeur de p.
Valeur de p ajustée
La valeur de p ajustée indique les paires, dans une famille de comparaisons, qui diffèrent de manière significative. L'ajustement limite le taux d'erreur famille au niveau d'alpha que vous indiquez. Si vous utilisez une valeur de p standard pour des comparaisons multiples, le taux d'erreur famille augmente à chaque ajout de comparaison.
Lorsque vous effectuez des comparaisons multiples, il est important de prendre en considération le taux d'erreur famille, car le risque de faire une erreur de 1ère espèce lors d'une série de comparaisons est plus élevé que le taux d'erreur de chacune des comparaisons individuelles.
Interprétation
Si la valeur de p ajustée est inférieure à alpha, rejetez l'hypothèse nulle et concluez-en que la différence dans une paire de moyennes de groupes est statistiquement significative. La valeur de p ajustée représente également le plus petit taux d'erreur famille auquel une hypothèse nulle donnée est rejetée.
Graphique des intervalles pour les différences de moyennes
Utilisez les intervalles de confiance afin de déterminer les étendues probables pour les différences et d'évaluer la signification concrète de ces différences. Le graphique présente un ensemble d'intervalles de confiance pour la différence entre des paires de moyennes. Les intervalles de confiance qui ne contiennent pas la valeur zéro indiquent une différence moyenne qui est statistiquement significative.
En fonction de la méthode de comparaison choisie, le graphique compare différentes paires de groupes et affiche l'un des types d'intervalles de confiance suivants.
-
Niveau de confiance individuel
Pourcentage d'occurrences, dans un même intervalle de confiance, de la différence réelle entre une paire de moyennes de groupes si l'étude était répétée plusieurs fois.
-
Niveau de confiance simultané
Il s'agit du pourcentage d'occurrences, dans un ensemble d'intervalles de confiance, des différences réelles pour toutes les comparaisons de groupes si l'étude est répétée plusieurs fois.
Le contrôle du niveau de confiance simultané est particulièrement important lorsque vous réalisez plusieurs comparaisons. Si vous ne le contrôlez pas, la probabilité qu'au moins un intervalle de confiance ne contienne pas la différence réelle augmente avec le nombre de comparaisons.
Pour plus d'informations, reportez-vous à la rubrique Présentation des niveaux de confiance individuel et simultané dans les comparaisons multiples.
Vous pouvez effectuer une analyse par comparaison multiple de termes aléatoires pour déterminer les niveaux du terme significativement différents des autres niveaux. Par exemple, si vous étudiez l'efficacité d'un médicament sur une maladie particulière, le sujet représente généralement un facteur aléatoire significatif. Vous pouvez utiliser des comparaisons multiples pour déterminer si le médicament a eu des effets différents sur des sujets spécifiques (il a peut-être rendu l'un d'entre eux plus malade).
Interprétation
Utilisez les intervalles de confiance pour évaluer les différences entre les moyennes de groupes.
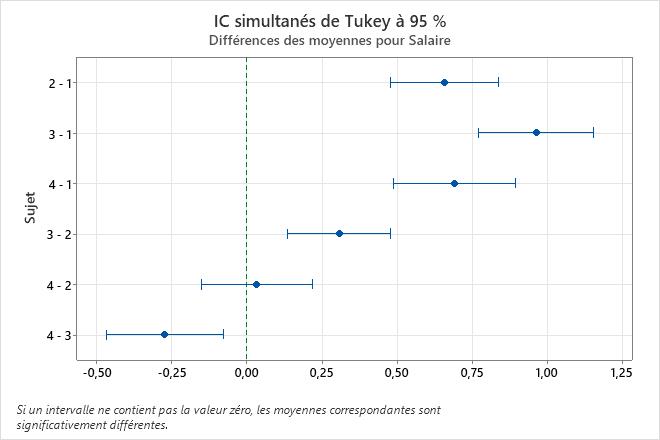
Tests de simultanéité de Tukey pour les différences des moyennes
| Différence des niveaux Sujet | Différence des moyennes | Erreur type de la différence | IC simultané à 95 % | Valeur de T | Valeur de p ajustée |
|---|---|---|---|---|---|
| 2 - 1 | 0,6567 | 0,0664 | (0,4768; 0,8366) | 9,89 | 0,000 |
| 3 - 1 | 0,9633 | 0,0708 | (0,7715; 1,1551) | 13,60 | 0,000 |
| 4 - 1 | 0,6900 | 0,0750 | (0,4870; 0,8930) | 9,20 | 0,000 |
| 3 - 2 | 0,3067 | 0,0632 | (0,1356; 0,4777) | 4,86 | 0,000 |
| 4 - 2 | 0,0333 | 0,0678 | (-0,1502; 0,2169) | 0,49 | 0,960 |
| 4 - 3 | -0,2733 | 0,0721 | (-0,4686; -0,0781) | -3,79 | 0,003 |
- L'intervalle de confiance pour la différence entre les moyennes des sujets 4 et 2 s'étend de -0,1502 à 0,2169. Cette étendue comprend la valeur zéro, ce qui indique que la différence n'est pas statistiquement significative.
- Les intervalles de confiance pour les paires de moyennes restantes ne comprennent pas la valeur zéro, ce qui indique que les différences sont statistiquement significatives.
- Le niveau de confiance simultané à 95 % indique que vous pouvez être sûr à 95 % que tous les intervalles de confiance contiennent les différences réelles.
- Le tableau indique que le niveau de confiance individuel est de 98,94 %. Ce résultat indique que vous pouvez être sûr à 98,94 % que chaque intervalle individuel contient la différence réelle dans une paire spécifique de moyennes de groupes.
- Le niveau de confiance individuel pour chaque comparaison génère collectivement le niveau de confiance simultané à 98,94 % pour les six comparaisons.
