Que sont les composantes de niveau et de tendance pour le lissage exponentiel double ?

Le lissage exponentiel double emploie une composante de niveau et une composante de tendance par période. Il utilise deux pondérations, ou paramètres de lissage, pour mettre à jour les composantes à chaque période. Les équations de lissage exponentiel double sont les suivantes :

L_t = α Y_t + (1 - α) [L_t-1 + T_t-1]
T_t = γ[L_t - L_t-1] + (1 - γ) T_t-1
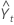= L_t-1 + T_t-1

où L_t est le niveau à l'instant t, α est la pondération du niveau, T_t est la tendance à l'instant t, γ est la pondération de la tendance, Y_t est la valeur des données à l'instant t et 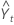est la valeur ajustée, ou prévision anticipée, à l'instant t.

La première observation porte le numéro 1. Pour pouvoir poursuivre, les estimations de niveau et de tendance à l'instant zéro doivent ensuite être initialisées. La méthode d'initialisation utilisée pour déterminer les valeurs lissées peut être obtenue de deux façons : avec des pondérations générées par Minitab ou avec des pondérations que vous définissez.

Pondérations ARIMA optimisées	Pondérations spécifiées
Minitab ajuste un modèle ARIMA (0,2,2) aux données afin de réduire la somme des erreurs quadratiques. Les composantes de niveau et de tendance sont ensuite initialisées par prévision descendante.	Minitab ajuste un modèle de régression linéaire aux données de séries chronologiques (variable y) en fonction du temps (variable x). La constante de cette régression est l'estimation initiale de la composante de niveau, tandis que le coefficient de pente est l'estimation initiale de la composante de tendance.

Si vous spécifiez des pondérations qui correspondent à un modèle ARIMA (0,2,2) à racines égales, la méthode de Holt se rapproche de la méthode de Brown.