Méthodes d'analyse de séries chronologiques

Les méthodes de prévision simple et de lissage modélisent les composantes d'une série qui sont faciles à observer sur un diagramme de série chronologique. Cette approche décompose les données en composantes, puis étend les estimations de ces composantes dans le temps pour fournir des prévisions. Vous pouvez choisir entre des méthodes statiques, comme l'analyse de tendance et la décomposition, et des méthodes dynamiques, comme la moyenne mobile, le lissage exponentiel simple et double ou la méthode de Winters. Les méthodes statiques ont des composantes invariantes dans le temps. Les méthodes dynamiques ont des composantes variables dans le temps et les estimations sont mises à jour en utilisant les valeurs voisines.

Les deux méthodes peuvent être utilisées conjointement, ce qui signifie que vous pouvez choisir une méthode statique pour modéliser une composante, et une méthode dynamique pour modéliser une autre composante. Par exemple, vous pouvez ajuster une tendance statique au moyen de l'analyse de tendance et effectuer une modélisation dynamique de la composante saisonnière des valeurs résiduelles au moyen de la méthode de Winters. Ou alors, vous pouvez ajuster un modèle saisonnier statique à l'aide d'une décomposition, et effectuer une modélisation dynamique des composantes de tendance dans les valeurs résiduelles au moyen d'un lissage exponentiel double. Vous pouvez également appliquer conjointement une analyse de tendance et une décomposition, de manière à utiliser la plus large sélection possible de modèles de tendances offerts par l'analyse de tendance. L'un des inconvénients de l'utilisation conjointe des deux méthodes est que les intervalles de confiance ne sont pas valides pour les prévisions.

Pour chacune de ces méthodes, le tableau ci-dessous fournit un récapitulatif et un graphique des ajustements et des prévisions pour des données courantes.

Analyse de tendance

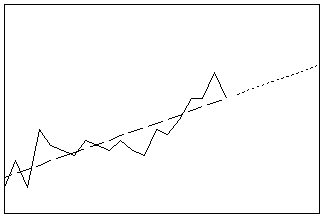
Ajuste un modèle général de tendance aux données d'une série chronologique. Sélectionnez un modèle de tendance linéaire, quadratique, un modèle à croissance ou décroissance exponentielle, ou un modèle en courbe en S. Utilisez cette procédure pour ajuster la tendance lorsque la série ne comporte pas de composante saisonnière.

Prévisions :

• Longueur : longue
• Profil : extension de la droite de tendance

Décomposition

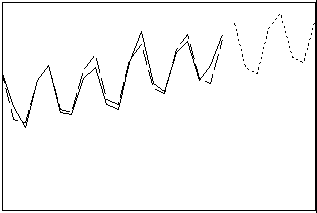
Décompose les séries chronologiques en composantes de tendance linéaire et en composantes saisonnières, ainsi qu'en erreur. Indiquez si la composante saisonnière est additive ou multiplicative par rapport à la tendance. Utilisez cette procédure lorsque la série comporte une composante saisonnière ou si vous souhaitez examiner la nature des composantes.

Prévisions :

• Longueur : longue
• Profil : tendance avec effets saisonniers

Moyenne mobile

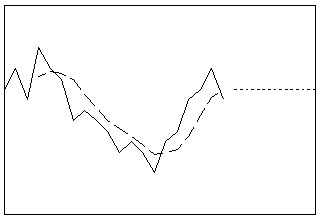
Lisse les données en établissant les moyennes des observations consécutives d'une série. Vous pouvez utiliser cette procédure lorsque les données n'ont pas de composante de tendance. Si vous avez une composante saisonnière, définissez la longueur de la moyenne mobile de sorte que celle-ci soit égale à la longueur du cycle saisonnier.

Prévisions :

• Longueur : courte
• Profil : ligne plate

Lissage exponentiel simple

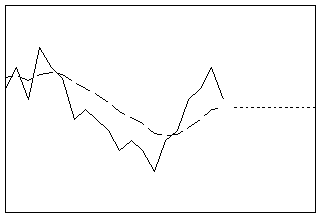
Lisse vos données à l'aide de la formule de prévision anticipée ARIMA (0, 1, 1) optimale. Cette procédure fonctionne mieux lorsqu'il n'y a pas ni composante de tendance ni composante saisonnière. La seule composante dynamique dans un modèle à moyenne mobile est le niveau.

Prévisions :

• Longueur : courte
• Profil : ligne plate

Lissage exponentiel double

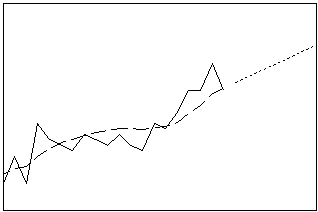
Lisse vos données à l'aide de la formule de prévision anticipée ARIMA (0, 2, 2) optimale. Cette procédure peut fonctionner parfaitement lorsqu'il y a une tendance, mais elle peut aussi servir de méthode générale de lissage. Le lissage exponentiel double calcule les estimations dynamiques pour deux composantes : niveau et tendance.

Prévisions :

• Longueur : courte
• Profil : ligne droite avec une pente égale à la dernière estimation de tendance

Méthode de Winters

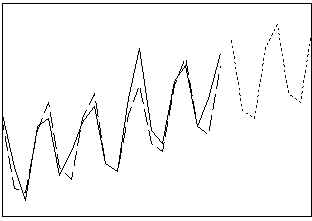
Lisse les données par la méthode de lissage exponentiel de Holt-Winters. Utilisez cette procédure lorsqu'il existe une tendance et des effets saisonniers, ces deux composantes étant additives ou multiplicatives. La méthode de Winters calcule des estimations dynamiques pour trois composantes : niveau, tendance et effet saisonnier.

Prévisions :

• Longueur : de courte à moyenne
• Profil : tendance avec effets saisonniers

La modélisation ARIMA (moyenne mobile autorégressive intégrée) fait aussi appel aux schémas présents dans les données, mais ces schémas peuvent ne pas être facilement visibles sur les diagrammes. A la place, la modélisation ARIMA utilise des fonctions de différentiation, d'autocorrélation et d'autocorrélation partielle pour aider à identifier un modèle acceptable.

La modélisation ARIMA peut servir à modéliser différentes séries chronologiques, avec ou sans tendance et/ou composante saisonnière, et à fournir des prévisions. Le profil de prévision dépend du modèle ajusté. L'avantage de la modélisation ARIMA sur les méthodes de prévision simple et de lissage est que son adaptation aux données s'avère beaucoup plus souple. Toutefois, l'identification et l'ajustement d'un modèle peut être une opération longue, et la modélisation ARIMA ne peut pas être facilement automatisée.

Différences

Calcule les différences entre les valeurs des données d'une série chronologique. Si un modèle ARIMA doit être ajusté alors que les données comportent une tendance ou des effets saisonniers, le calcul des différences dans les données est une étape courante de l'évaluation préférentielle des modèles ARIMA. Les différences servent à simplifier la structure de la corrélation et à révéler les schémas sous-jacents.

Décalage

Calcule et stocke les décalages d'une série chronologique. Lorsque vous décalez une série chronologique, Minitab déplace les valeurs d'origine vers le bas de la colonne et insère des valeurs manquantes en haut de la colonne. Le nombre de valeurs manquantes inséré dépend de l'amplitude du décalage.

Autocorrélation

Calcule et crée un graphique d'autocorrélations d'une série chronologique. Une autocorrélation est la corrélation entre les observations d'une série chronologique séparées par k unités de temps. Le diagramme des autocorrélations est dénommé fonction d'autocorrélation (ACF). Visualisez l'ACF pour obtenir une aide pour le choix des termes à inclure dans un modèle ARIMA.

Autocorrélation partielle

Calcule et crée un graphique des autocorrélations partielles d'une série chronologique. Les autocorrélations partielles, comme les autocorrélations, sont des corrélations entre des jeux de paires de données ordonnées d'une série chronologique. Comme avec les corrélations partielles dans le cas d'une régression, les autocorrélations partielles donnent une mesure de l'importance des relations avec les autres termes expliqués. Une autocorrélation partielle avec un décalage négatif de k est la corrélation entre les valeurs résiduelles d'un modèle autorégressif à l'instant t et les valeurs observées avec un décalage négatif k avec les termes de tous les décalages négatifs présents dans le modèle autorégressif. Le graphique d'autocorrélations partielles est dénommé fonction d'autocorrélation partielle (PACF). Visualisez la PACF pour obtenir une aide pour le choix des termes à inclure dans un modèle ARIMA.

Intercorrélation

Calcule et crée un graphique des corrélations entre deux séries chronologiques.

ARIMA

Ajuste un modèle ARIMA de Box-Jenkins à une série chronologique. Dans l'acronyme ARIMA (Autoregressive Integrated Moving Average, en français Moyenne mobile autorégressive intégrée), les termes "moyenne mobile", "autorégressive" et "intégrée" font référence aux étapes de filtrage effectuées lors du calcul du modèle ARIMA. Le filtrage se poursuit jusqu'à ce qu'il ne reste que des éléments parasites (bruit) aléatoires. Utilisez l'ARIMA pour modéliser le comportement d'une série chronologique et pour générer des prévisions.