Assistance de Minitab® 

Méthodes et formules pour la fonction Méthode de Winters

En savoir plus sur Minitab
Sélectionnez la méthode ou la formule de votre choix.

Sur ce thème

Multiplicatif

Formule

Le modèle multiplicatif est le suivant :

  • Lt = α (Yt / St–p) + (1 – α) [Lt–1 + Tt–1]
  • Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
  • St = δ (Yt / Lt) + (1 – δ) St–p
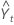  • = (Lt–1 + Tt–1) St–p

Notation

TermeDescription
Ltniveau à l'instant t, α est la pondération du niveau
Tttendance à l'instant t,
γpondération pour la tendance
Stcomposante saisonnière à l'instant t
δpondération pour la composante saisonnière
ppériode saisonnière
Ytvaleur de données à l'instant t
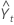valeur ajustée, ou prévision une période à l'avance, à l'instant t

Méthode de calcul des valeurs initiales du niveau et de la tendance pour les modèles multiplicatifs

La méthode suivante suppose une durée saisonnière supérieure à 4.

  1. Trouvez la moyenne, le minimum et le maximum des données. Pour cet exemple :
    • Moyenne = 554,208
    • Min = 1
    • Max = 1498,47
  2. Pour chaque ligne de données, calculez :
  3. Passons N égale à la durée saisonnière. Pour cet exemple, N = 12.
  4. Exécutez la régression avec les premières "valeurs temporaires" N (calculées à l’étape 2) comme variable Y, et d’un vecteur de 1 à N comme variable X. Donc pour cet exemple :
    Y X
    4104,36 1
    4104,36 2
    4630,36 3
    4922,80 4
    4822,40 5
    5601,83 6
    4891,77 7
    4604,44 8
    4411,26 9
    4123,66 10
    4104,36 11
    4104,36 12

    La pente de la ligne de régression est la valeur initiale de la tendance.

  5. Ajustez l'ordonnée à l'origine pour la ligne de régression en soustrayant :

L'ordonnée à l'origine pour vos données est 4705,24. Soustrayez le 4103,36 de l'ordonnée à l'origine pour obtenir une ordonnée à l'origine ajustée de 601,879. Cette ordonnée à l'origine ajustée est la valeur initiale pour le niveau.

Additif

Formule

Le modèle additif est le suivant :
  • Lt = α (Yt – St–p) + (1 – α) [Lt–1 + Tt–1]
  • Tt = γ [Lt – Lt–1] + (1 – γ) Tt–1
  • St = δ (Yt – Lt) + (1 – δ) St–p
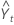  • = Lt–1 + Tt–1 + St–p

Notation

TermeDescription
Ltniveau à l'instant t, α est la pondération du niveau
Tttendance à l'instant t,
γpondération pour la tendance
Stcomposante saisonnière à l'instant t
δpondération pour la composante saisonnière
ppériode saisonnière
Ytvaleur de données à l'instant t
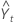valeur ajustée, ou prévision une période à l'avance, à l'instant t

Méthode de calcul des valeurs initiales pour le niveau et la tendance pour les modèles additifs

La méthode suivante suppose une durée saisonnière supérieure à 4.

  1. Passons N égale à la durée saisonnière. Pour cet exemple, N = 12.
  2. Exécutez la régression avec les premières valeurs de données N comme variable Y, et un vecteur de 1 à N comme variable X. Donc pour cet exemple :
    Y X
    1,00 1
    1,00 2
    527,00 3
    819,45 4
    719,04 5
    1498,47 6
    788,42 7
    501,08 8
    307,90 9
    20,30 10
    1,00 11
    1,00 12

    La pente de la ligne de régression est la valeur initiale de la tendance. L'ordonnée à l'origine de la ligne de régression est la valeur initiale pour le niveau.

Méthode de calcul des valeurs initiales des indices saisonniers pour les modèles additifs

La méthode suivante suppose une durée saisonnière supérieure à 4.

  1. Exécutez la régression avec les valeurs de données comme variable Y, et un vecteur de 1 à 24 comme variable X. Donc pour cet exemple :
    Y X
    1,00 1
    1,00 2
    527,00 3
    819,45 4
    719,04 5
    1498,47 6
    788,42 7
    501,08 8
    307,90 9
    20,30 10
    1,00 11
    1,00 12
    83,00 13
    668,21 14
    1121,28 15
    1386,84 16
    1031,18 17
    988,60 18
    1380,30 19
    1005,97 20
    233,69 21
    211,87 22
    2,00 23
    2,40 24

    Utilisez les valeurs résiduelles de ce modèle de régression à l’étape suivante

  2. Exécutez la régression avec les valeurs résiduelles comme variable Y, et 12 variables d’indicateur (z.1 à z.12) comme variables X. Adaptez le modèle de régression sans un terme d'ordonnée à l'origine (constante). Donc pour cet exemple :
    Valeurs résiduelles z.1 z.2 z.3 z.4 z.5 z.6 z.7 z.8 z.9 z.10 z.11 z.12
    -508,261 1 0 0 0 0 0 0 0 0 0 0 0
    -512,170 0 1 0 0 0 0 0 0 0 0 0 0
    9,926 0 0 1 0 0 0 0 0 0 0 0 0
    298,460 0 0 0 1 0 0 0 0 0 0 0 0
    194,145 0 0 0 0 1 0 0 0 0 0 0 0
    969,667 0 0 0 0 0 1 0 0 0 0 0 0
    255,705 0 0 0 0 0 0 1 0 0 0 0 0
    -35,538 0 0 0 0 0 0 0 1 0 0 0 0
    -232,625 0 0 0 0 0 0 0 0 1 0 0 0
    -524,137 0 0 0 0 0 0 0 0 0 1 0 0
    -547,346 0 0 0 0 0 0 0 0 0 0 1 0
    -551,254 0 0 0 0 0 0 0 0 0 0 0 1
    -473,161 1 0 0 0 0 0 0 0 0 0 0 0
    108,141 0 1 0 0 0 0 0 0 0 0 0 0
    557,303 0 0 1 0 0 0 0 0 0 0 0 0
    818,952 0 0 0 1 0 0 0 0 0 0 0 0
    459,378 0 0 0 0 1 0 0 0 0 0 0 0
    412,890 0 0 0 0 0 1 0 0 0 0 0 0
    800,684 0 0 0 0 0 0 1 0 0 0 0 0
    422,451 0 0 0 0 0 0 0 1 0 0 0 0
    -353,739 0 0 0 0 0 0 0 0 1 0 0 0
    -379,468 0 0 0 0 0 0 0 0 0 1 0 0
    -593,247 0 0 0 0 0 0 0 0 0 0 1 0
    Les coefficients de ce modèle de régression sont les valeurs initiales des indices saisonniers. Les coefficients sont :
    Période COEF1
    1 -490,711
    2 -202,014
    3 283,615
    4 558,706
    5 326,762
    6 691,278
    7 528,195
    8 193,456
    9 -293,182
    10 -451,803
    11 -570,297
    12 -574,005
    Remarque

    Les variables de l’indicateur z.1 à z.12 indiquent à quel mois de la période appartient chaque point de données. La variable z.1 est par exemple égale à 1 pour le premier mois de la période, et à 0 autrement.

Ajustement de modèles

La méthode de Winters emploie une composante de niveau, une composante de tendance et une composante saisonnière pour chaque période. Cette méthode utilise trois pondérations, ou paramètres de lissage, pour mettre à jour les composantes à chaque période. Les valeurs initiales pour les composantes de niveau et de tendance sont obtenues par régression linéaire dans le temps. Les valeurs initiales pour la composante saisonnière sont obtenues à partir d'une régression à variable indicatrice utilisant des données sans tendance.

Prévision

La méthode de Winters utilise les composantes de niveau, de tendance et de saisonnalité pour effectuer des prévisions. La méthode de Winters utilise également les données allant jusqu'à l'origine de la prévision pour générer des prévisions.

Formule

La prévision pour un point à l'instant t à m périodes dans le futur est égale à :
  • Méthode multiplicative : (Lt + mTt) * St + m −p
  • Méthode additive : Lt + mTt +St + m −p

Notation

TermeDescription
Ltniveau
Tttendance à l'instant t
TermeDescription
St + m −pcomposante de saisonnalité pour la même période, l'année précédente

MAPE

La valeur MAPE (pourcentage d'erreur absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude sous forme de pourcentage.

Formule

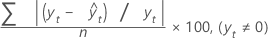
Notation

TermeDescription
yt valeur réelle à l'instant t
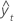valeur ajustée
n nombre d'observations

MAD

La valeur MAD (écart absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude dans les mêmes unités que les données, ce qui aide à conceptualiser l'importance de l'erreur.

Formule

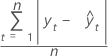
Notation

TermeDescription
yt valeur réelle à l'instant t
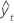valeur ajustée
n nombre d'observations

MSD

La valeur MSD (écart quadratique moyen) est toujours calculée à l'aide du même dénominateur, n, indifféremment du modèle. Par rapport à MAD, la mesure MSD est une mesure plus sensible des erreurs de prévision inhabituellement élevées.

Formule

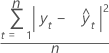
Notation

TermeDescription
yt valeur réelle à l'instant t
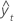valeur ajustée
n nombre d'observations
Copyright © 2024 Minitab, LLC. All rights Reserved.