Sur ce thème
Linéaire
Formule
le modèle de tendance linéaire est le suivant :
Yt = β0 + β1t + et
Notation
| Terme | Description |
|---|---|
| β0 | constante |
| β1 | variation moyenne d'une période à la suivante |
| t | valeur de l'unité de temps |
| et | terme d'erreur |
Croissance exponentielle
Formule
Le modèle de tendance à croissance exponentielleprend en compte une croissance ou une décroissance exponentielle. Par exemple, un compte d'épargne peut présenter une croissance exponentielle.
Yt = β0 * β1t * et
Notation
| Terme | Description |
|---|---|
| β0 | constante |
| β1 | coefficient |
| t | valeur de l'unité de temps |
| et | terme d'erreur |
Quadratique
Formule
Le modèle de tendance quadratique, qui peut rendre compte d'une courbure simple dans les données, est le suivant :
Yt = β0 + β1t + β2t2 + et
Notation
| Terme | Description |
|---|---|
| β0 | constante |
| β1 et β2 | coefficients |
| t | valeur de l'unité de temps |
| et | terme d'erreur |
Courbe S
Formule
Les données ont une forme en S, ce qui indique que le sens de la variation change au cours du temps.
Yt = 10a / (β0 + β1β2t)
Notation
| Terme | Description |
|---|---|
| β0 | constante |
| β1 et β2 | coefficients |
| t | valeur de l'unité de temps |
Pondérations
Si vous fournissez des coefficients provenant de l'ajustement d'une précédente analyse de tendance, Minitab effectue une analyse de tendance pondérée. Si le facteur de pondération d'un coefficient déterminé est α, Minitab estime le nouveau coefficient de la façon suivante :
Formule
αp1 + (1 – α)p2
Notation
| Terme | Description |
|---|---|
| p1 | coefficient estimé à partir des données actuelles |
| p2 | coefficient précédent |
Prévisions
Minitab utilise l'équation de tendance pour effectuer des prévisions pour des valeurs de temps spécifiques. Les données antérieures à la prévision d'origine servent à ajuster la tendance.
MAPE
La valeur MAPE (pourcentage d'erreur absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude sous forme de pourcentage.
Formule
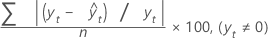
Notation
| Terme | Description |
|---|---|
| yt | valeur réelle à l'instant t |
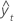 | valeur ajustée |
| n | nombre d'observations |
MAD
La valeur MAD (écart absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude dans les mêmes unités que les données, ce qui aide à conceptualiser l'importance de l'erreur.
Formule
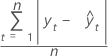
Notation
| Terme | Description |
|---|---|
| yt | valeur réelle à l'instant t |
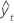 | valeur ajustée |
| n | nombre d'observations |
MSD
La valeur MSD (écart quadratique moyen) est toujours calculée à l'aide du même dénominateur, n, indifféremment du modèle. Par rapport à MAD, la mesure MSD est une mesure plus sensible des erreurs de prévision inhabituellement élevées.
Formule
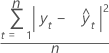
Notation
| Terme | Description |
|---|---|
| yt | valeur réelle à l'instant t |
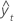 | valeur ajustée |
| n | nombre d'observations |
