Méthodes et formules pour la fonction Lissage exponentiel simple

Les valeurs lissées sont obtenues de deux manières : avec un poids optimal généré par Minitab ou un poids que vous spécifiez.

Pondération ARIMA optimale

1. Minitab s’adapte à un modèle ARIMA (0,1,1) sans constante et stocke les ajustements.
2. La valeur initiale lissée pour l’analyse de lissage exponentiel simple est le premier ajustement non manquant du modèle ARIMA.
3. Comme les ajustements sont en unité à retard unique, Minitab utilise le backcasting pour calculer la valeur initiale d’ajustement (au moment un) :
   • Valeur initiale ajustée = [La première valeur lissée – α (première valeur de données)] / (1 – α)

Notation

Pondération indiquée

1. Minitab utilise la moyenne des six (ou N, si N < 6) premières observations pour la valeur initiale lissée (à l'instant zéro). De même, Minitab utilise la moyenne des six (ou N, si N < 6) premières observations pour la valeur ajustée initiale (à l'instant un). Ajustement(i) = Lissé (i – 1).
2. Les valeurs lissées suivantes sont calculées à partir de la formule :
   • Valeur lissée au temps t = α (données à t) + (1 – α) (valeur lissée au temps t – 1)

Notation

La valeur ajustée à l'instant t est la valeur lissée à l'instant t – 1. Les prévisions sont les valeurs ajustées à l'origine de la période de prévision. Si vous effectuez une prévision à 10 unités de temps de distance, les valeurs prévues pour chaque instant seront les valeurs ajustées à l'instant d'origine. Les données jusqu'à l'instant d'origine sont utilisées pour lissage.

Dans la prévision naïve, la valeur prévue à l'instant t est la valeur des données à l'instant t – 1. En utilisant le lissage exponentiel simple avec une pondération de 1, vous obtenez une prévision naïve.

Formule

La valeur de 1,25 est une constante de proportionnalité approximative de l'écart type par rapport à l'écart absolu moyen. Ainsi, 1,25 x MAD est à peu près égal à l'écart type.

La valeur MAPE (pourcentage d'erreur absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude sous forme de pourcentage.

Formule

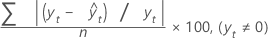
Notation

Terme	Description
yt	valeur réelle à l'instant t
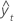	valeur ajustée
n	nombre d'observations

La valeur MAD (écart absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude dans les mêmes unités que les données, ce qui aide à conceptualiser l'importance de l'erreur.

Formule

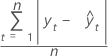
Notation

Terme	Description
yt	valeur réelle à l'instant t
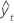	valeur ajustée
n	nombre d'observations

La valeur MSD (écart quadratique moyen) est toujours calculée à l'aide du même dénominateur, n, indifféremment du modèle. Par rapport à MAD, la mesure MSD est une mesure plus sensible des erreurs de prévision inhabituellement élevées.

Formule

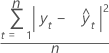
Notation

Terme	Description
yt	valeur réelle à l'instant t
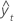	valeur ajustée
n	nombre d'observations