Méthodes et formules pour la fonction Moyenne mobile

Pour calculer une moyenne mobile, Minitab fait la moyenne de groupes d'observations consécutifs d'une série. Par exemple, supposons qu'une série commence par les nombres 4, 5, 8, 9 et 10 et que vous utilisez une longueur de moyenne mobile de 3. Les deux premières valeurs de moyenne mobile sont manquantes. La troisième valeur de moyenne mobile est la moyenne de 4, 5 et 8 ; la quatrième valeur est la moyenne de 5, 8 et 9 ; la cinquième valeur est la moyenne de 8, 9 et 10.

Par défaut, les valeurs de la moyenne mobile sont placées à la période pour laquelle elles sont calculées. Par exemple, pour une moyenne mobile ayant une longueur égale à 3, la première valeur numérique de la moyenne mobile est placée à la période 3, la suivante à la période 4, et ainsi de suite.

Si vous cochez cette option, Minitab place les valeurs des moyennes mobiles au centre plutôt qu'à la fin de l'étendue. Cela place les valeurs de la moyenne mobile dans leurs positions centrales dans le temps.

Si la longueur de la moyenne mobile est impaire

Supposons que la longueur d'une moyenne mobile soit égale à 3. Dans ce cas, Minitab place la première valeur numérique de moyenne mobile sur la période 2, la suivante sur la période 3, et ainsi de suite. Dans ce cas, les valeurs de moyenne mobile pour la première et la dernière période sont manquantes (*).

Si la longueur de la moyenne mobile est paire

Supposons que la longueur de la moyenne mobile soit égale à 4. Comme vous ne pouvez pas placer une valeur de moyenne mobile sur la période 2,5, Minitab calcule la moyenne des quatre premières valeurs et la nomme MB1. Minitab calcule ensuite la moyenne des quatre valeurs suivantes et la nomme MB2. La moyenne de ces deux valeurs est le nombre placé sur la période 3 par Minitab. Dans ce cas, les valeurs de moyenne mobile des deux premières et des deux dernières périodes sont manquantes (*).

La valeur ajustée à l'instant t est la moyenne mobile non centrée à l'instant t - 1. Les prévisions sont les valeurs ajustées calculées pour l'instant d'origine de la prévision. Si vous effectuez une prévision à 10 unités de temps de distance, les valeurs prévues pour chaque instant seront les valeurs ajustées à l'instant d'origine. Les données précédant cet instant d'origine sont utilisées pour le calcul des moyennes mobiles.

Vous pouvez utiliser la méthode de la moyenne linéaire mobile en calculant des moyennes mobiles consécutives. Cette opération est souvent effectuée lorsqu'il existe une tendance dans les données. Tout d'abord, calculez et stockez la moyenne mobile de la série initiale. Ensuite, calculez et stockez la moyenne mobile de la colonne précédemment stockée pour obtenir une deuxième moyenne mobile.

Dans la prévision naïve, la valeur prévue pour l'instant t est la valeur des données à l'instant t – 1. Vous obtenez une prévision naïve si vous utilisez la procédure de moyenne mobile avec une longueur de moyenne mobile de 1.

Formule

Limite supérieure = Prévision + 1,96 ×

Limite inférieure = Prévision – 1,96 ×

Notation

La valeur MAPE (pourcentage d'erreur absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude sous forme de pourcentage.

Formule

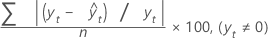
Notation

Terme	Description
yt	valeur réelle à l'instant t
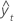	valeur ajustée
n	nombre d'observations

La valeur MAD (écart absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude dans les mêmes unités que les données, ce qui aide à conceptualiser l'importance de l'erreur.

Formule

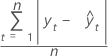
Notation

Terme	Description
yt	valeur réelle à l'instant t
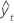	valeur ajustée
n	nombre d'observations

La valeur MSD (écart quadratique moyen) est toujours calculée à l'aide du même dénominateur, n, indifféremment du modèle. Par rapport à MAD, la mesure MSD est une mesure plus sensible des erreurs de prévision inhabituellement élevées.

Formule

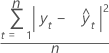
Notation

Terme	Description
yt	valeur réelle à l'instant t
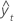	valeur ajustée
n	nombre d'observations