Sur ce thème
Longueur
Nombre d'observations dans la série chronologique.
Nombre de valeurs manquantes
Nombre de valeurs manquantes dans la série chronologique.
Longueur de moyenne mobile
La longueur de moyenne mobile représente le nombre d'observations consécutives utilisées par Minitab pour calculer les moyennes mobiles. Par exemple, pour des données mensuelles, une valeur de 3 indique que la moyenne mobile de mars est calculée comme la moyenne des observations de mars, février et janvier
Moyenne mobile = 2
Moyenne mobile = 6
MAPE
La valeur MAPE (pourcentage d'erreur absolu moyen) exprime l'exactitude sous la forme d'un pourcentage de l'erreur. A ce titre, elle peut être plus facile à comprendre que les autres statistiques de mesure de l'exactitude. Par exemple, si la valeur MAPE est de 5, en moyenne, la prévision est erronée de 5 %.
Cependant, vous pouvez parfois constater une valeur MAPE élevée alors que le modèle semble correctement ajusté aux données. Dans ce cas, étudiez le diagramme pour savoir si des valeurs de données sont proches de 0. Etant donné que la statistique MAPE divise l'erreur absolue par les données réelles, les valeurs proches de 0 peuvent la faire augmenter de manière importante.
Interprétation
Utilisez cet outil pour comparer les valeurs ajustées de différents modèles de série chronologique. Plus les valeurs sont faibles, meilleur est l'ajustement. Si aucun même modèle ne réunit les valeurs les plus basses pour les 3 mesures d'exactitude, la statistique MAPE est généralement celle qui est privilégiée.
Les mesures d'exactitude reposent sur les valeurs résiduelles obtenues à partir de la période précédente. A chaque point dans le temps, le modèle est utilisé pour prévoir la valeur Y pour la prochaine période. La différence entre les valeurs prévues (valeurs résiduelles) et la valeur Y réelle est égale aux valeurs résiduelles obtenues à partir de la période précédente. De ce fait, les mesures de l'exactitude fournissent une indication de l'exactitude à attendre lorsque vous effectuez une prévision pour une période à partir de la fin des données. Ainsi, elles n'indiquent pas l'exactitude des prévisions au-delà d'une période. Si vous comptez utiliser le modèle pour effectuer des prévisions, vous ne devez pas vous fier uniquement aux mesures d'exactitude pour prendre une décision. Vous devez également examiner l'ajustement du modèle pour vous assurer qu'il suit étroitement les données, notamment à la fin de la série, et qu'il en est de même pour les prévisions.
MAD
L'écart absolu moyen (MAD) exprime l'exactitude dans les mêmes unités que les données, ce qui aide à conceptualiser l'importance de l'erreur. Les valeurs aberrantes ont moins d'effet sur le MAD que sur le MSD.
Interprétation
Utilisez cet outil pour comparer les valeurs ajustées de différents modèles de série chronologique. Plus les valeurs sont faibles, meilleur est l'ajustement.
Les mesures d'exactitude reposent sur les valeurs résiduelles obtenues à partir de la période précédente. A chaque point dans le temps, le modèle est utilisé pour prévoir la valeur Y pour la prochaine période. La différence entre les valeurs prévues (valeurs résiduelles) et la valeur Y réelle est égale aux valeurs résiduelles obtenues à partir de la période précédente. De ce fait, les mesures de l'exactitude fournissent une indication de l'exactitude à attendre lorsque vous effectuez une prévision pour une période à partir de la fin des données. Ainsi, elles n'indiquent pas l'exactitude des prévisions au-delà d'une période. Si vous comptez utiliser le modèle pour effectuer des prévisions, vous ne devez pas vous fier uniquement aux mesures d'exactitude pour prendre une décision. Vous devez également examiner l'ajustement du modèle pour vous assurer qu'il suit étroitement les données, notamment à la fin de la série, et qu'il en est de même pour les prévisions.
MSD
Le MSD (écart moyen quadratique), mesure l'exactitude des valeurs ajustées des séries chronologiques. Les valeurs aberrantes ont un effet plus important sur le MSD que sur le MAD.
Interprétation
Utilisez cet outil pour comparer les valeurs ajustées de différents modèles de série chronologique. Plus les valeurs sont faibles, meilleur est l'ajustement.
Les mesures d'exactitude reposent sur les valeurs résiduelles obtenues à partir de la période précédente. A chaque point dans le temps, le modèle est utilisé pour prévoir la valeur Y pour la prochaine période. La différence entre les valeurs prévues (valeurs résiduelles) et la valeur Y réelle est égale aux valeurs résiduelles obtenues à partir de la période précédente. De ce fait, les mesures de l'exactitude fournissent une indication de l'exactitude à attendre lorsque vous effectuez une prévision pour une période à partir de la fin des données. Ainsi, elles n'indiquent pas l'exactitude des prévisions au-delà d'une période. Si vous comptez utiliser le modèle pour effectuer des prévisions, vous ne devez pas vous fier uniquement aux mesures d'exactitude pour prendre une décision. Vous devez également examiner l'ajustement du modèle pour vous assurer qu'il suit étroitement les données, notamment à la fin de la série, et qu'il en est de même pour les prévisions.
Moyenne mobile
Les valeurs de moyenne mobile sont calculées à partir d'observations consécutives. Par exemple, pour des données mensuelles dont la longueur de moyenne mobile est de 3, la moyenne mobile de mars correspond à la moyenne des observations de mars, février et janvier.
Prévisions (également appelées valeurs ajustées)
La valeur prévue pour l'instant t est égale à la valeur de la moyenne mobile à l'instant t-1.
Les observations dont les valeurs prévues sont très différentes de la valeur observée peuvent être des valeurs aberrantes ou influentes. Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Envisagez de supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.
Error
Les valeurs d'erreur sont aussi appelées valeurs résiduelles. Les valeurs résiduelles correspondent aux différences entre les valeurs observées et les valeurs prévues.
Interprétation
Tracez un graphique des valeurs d'erreur pour déterminer si votre modèle est adapté. Ces valeurs peuvent fournir des informations utiles sur l'ajustement du modèle aux données. En règle générale, les valeurs d'erreur doivent être distribuées de manière aléatoire autour de 0 sans aucun schéma clair ni aucune valeur aberrante.
Période
Minitab affiche la période lorsque vous générez des prévisions. La période est l'unité de temps de la prévision. Par défaut, les prévisions commencent à la fin des données.
Prévision
Les prévisions sont les valeurs ajustées obtenues à partir du modèle de série chronologique. Minitab affiche le nombre de prévisions que vous indiquez. Les prévisions commencent soit à la fin des données, soit au point d'origine que vous avez indiqué.
Interprétation
Utilisez les prévisions pour prévoir la valeur d'une variable pour une période donnée. Par exemple, la responsable d'un entrepôt peut modéliser la quantité de produit qu'elle a besoin de commander pour les 3 mois à venir, en fonction des 60 derniers mois de commande.
Examinez les valeurs ajustées et les prévisions dans le diagramme pour déterminer si ces dernières ont des chances d'être exactes. Les prévisions doivent généralement suivre les données à la fin de la série. Si les valeurs ajustées s'écartent des valeurs des données à la fin de la série, les prévisions peuvent ne pas être exactes. Les prévisions obtenues à partir de la moyenne mobile étant constantes, il est important que les données ne présentent aucune tendance avant les prévisions. S'il existe une tendance avant les prévisions, celles-ci risquent de ne pas être exactes.
Les prévisions obtenues à partir de la moyenne mobile sont très prudentes, car elles se fondent uniquement sur la dernière estimation du niveau et non sur l'estimation de la tendance. En général, vous ne devez pas effectuer de prévisions au-delà de 6 périodes dans l'avenir.
Limites inférieure et supérieure
Les limites de prédiction inférieure et supérieure forment un intervalle de prédiction pour chaque prévision. L'intervalle de prédiction est une étendue de valeurs probables pour les prévisions. Par exemple, avec un intervalle de prédiction à 95 %, vous pouvez être sûr à 95 % que l'intervalle de prédiction contient la prévision au moment indiqué.
Diagramme de moyenne mobile
Le diagramme de moyenne mobile affiche les observations en fonction du temps. Le diagramme inclut les valeurs ajustées calculées à partir des moyennes mobiles, les prévisions, la longueur des moyennes mobiles et les mesures d'exactitude. Vous pouvez également afficher les valeurs lissées à la place des valeurs ajustées.
Interprétation
- Si le modèle est ajusté aux données, vous pouvez utiliser la fonction Lissage exponentiel simple et comparer les deux modèles.
- Si le modèle n'est pas ajusté aux données, recherchez des tendances ou une saisonnalité dans le diagramme. S'il existe une tendance ou une saisonnalité, vous devez utiliser une autre analyse de série chronologique. Pour plus d'informations, reportez-vous à la rubrique Quelle analyse de série chronologique dois-je utiliser ?.
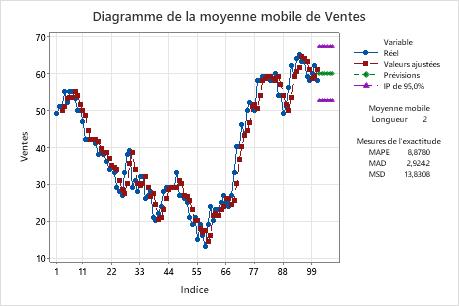
Sur ce diagramme de lissage, les valeurs ajustées suivent étroitement les données, ce qui indique que le modèle est ajusté aux données.
Histogramme des valeurs résiduelles
L'histogramme des valeurs résiduelles présente la loi de distribution des valeurs résiduelles pour toutes les observations. Si le modèle est correctement ajusté aux données, les valeurs résiduelles doivent être réparties de manière aléatoire avec une moyenne de 0. Par conséquent, l'histogramme doit être a peu près symétrique autour de 0.
Droite de Henry des valeurs résiduelles
La droite de Henry des valeurs résiduelles affiche les valeurs résiduelles en fonction de leurs valeurs attendues lorsque la loi de distribution est normale.
Interprétation
Utilisez la droite de Henry des valeurs résiduelles pour déterminer si les valeurs résiduelles sont normalement distribuées. Notez cependant que cette analyse ne requiert pas que les valeurs résiduelles soient distribuées normalement.
Une courbe S implique une distribution aux extrémités allongées.
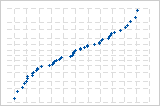
Une courbe S inversée implique une distribution aux extrémités écourtées.

Une courbe descendante implique une loi asymétrique à droite.

Quelques points situés loin de la ligne impliquent une distribution comportant des valeurs aberrantes.
Valeurs résiduelles en fonction des valeurs ajustées
Le diagramme des valeurs résiduelles en fonction des valeurs ajustées affiche les valeurs résiduelles sur l'axe des Y et les valeurs ajustées sur l'axe des X.
Interprétation
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour déterminer si les valeurs résiduelles ne sont pas biaisées et ont une variance constante. Idéalement, les points doivent être répartis de façon aléatoire de chaque côté de 0, sans schéma visible.
| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Curviligne | Un terme d'ordre supérieur manquant |
| Un point très éloigné de zéro | Une valeur aberrante |
Si vous constatez une variance non constante ou des schémas dans les valeurs résiduelles, vos prévisions risquent de ne pas être exactes.
Valeurs résiduelles en fonction de l'ordre
Le diagramme des valeurs résiduelles en fonction de l'ordre affiche les valeurs résiduelles dans l'ordre dans lequel elles ont été collectées.
Interprétation
Utilisez le diagramme des valeurs résiduelles en fonction de l'ordre pour déterminer l'exactitude des valeurs ajustées par rapport aux valeurs observées au cours de la période d'observation. Si les points suivent un schéma particulier, il se peut que le modèle ne soit pas ajusté aux données. Idéalement, les valeurs résiduelles sur le diagramme doivent être réparties de façon aléatoire autour de la ligne ajustée.
| Schéma | Ce que le schéma indique |
|---|---|
| Une tendance contante à long terme | Le modèle n'est pas ajusté aux données |
| Une tendance à court terme | Un décalage ou une modification dans le schéma |
| Un point très éloigné des autres | Une valeur aberrante |
| Un brusque décalage entre les points | Le schéma sous-jacent des données a changé |
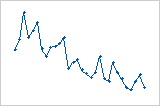
Les valeurs résiduelles diminuent systématiquement alors que l'ordre des observations augmente de gauche à droite.
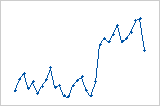
Il existe une variation soudaine des valeurs résiduelles entre les valeurs faibles (à gauche) et élevées (à droite).
Valeurs résiduelles en fonction des variables
Le diagramme des valeurs résiduelles en fonction des variables affiche les valeurs résiduelles en fonction d'une autre variable.
Interprétation
Utilisez le diagramme pour déterminer si la variable a systématiquement un effet sur la réponse. Si les valeurs résiduelles présentent des schémas, les autres variables sont associées à la réponse. Vous pouvez utiliser cette information comme fondement pour des études supplémentaires.
