Interpréter les principaux résultats pour Prévision avec le meilleur modèle ARIMA

Effectuez les étapes suivantes pour interpréter le processus de sélection du modèle et les résultats de l’analyse ARIMA. Les principaux résultats comprennent les statistiques de sélection du modèle, la valeur de p, les coefficients, les statistiques du chi carré de Ljung-Box et la fonction d’autocorrélation des résidus.

Sur ce thème

Etape 1 : Envisager d’autres modèles
Etape 2 : Déterminer si chaque terme du modèle est significatif
Etape 3 : Déterminer si votre modèle respecte l'hypothèse de l'analyse

Etape 1 : Envisager d’autres modèles

Le tableau Sélection du modèle affiche les critères de chaque modèle dans la recherche. Le tableau affiche l’ordre des termes où p est le terme autorégressif, d est le terme de différenciation et q est le terme de la moyenne mobile. Les termes saisonniers utilisent des lettres majuscules et les termes non saisonniers utilisent des lettres minuscules.

Utilisez les valeurs AIC, AICc et BIC pour comparer différents modèles. Les valeurs faibles sont les valeurs souhaitables. Cependant, le modèle avec la valeur la plus faible pour un ensemble de termes ne correspond pas nécessairement bien aux données. Utilisez des tests et des graphiques pour évaluer dans quelle mesure le modèle s’adapte aux données. Par défaut, les résultats ARIMA sont pour le modèle avec la meilleure valeur d’AICc.

Sélectionnez Sélectionner un autre modèle cette option pour ouvrir une boîte de dialogue qui inclut un tableau Sélection de modèle. Comparez les critères pour étudier des modèles ayant des performances similaires.

Utilisez la sortie ARIMA pour vérifier que les termes du modèle sont statistiquement significatifs et que le modèle répond aux hypothèses de l’analyse. Si aucun des modèles du tableau ne correspond bien aux données, considérez les modèles avec différents ordres de différenciation.

Considérez également un modèle alternatif lorsqu’un modèle alternatif fonctionne presque aussi bien que le meilleur modèle et a des ordres inférieurs pour les termes autorégressifs et de moyenne mobile. Un modèle avec moins de termes est plus facile à interpréter et peut avoir une meilleure capacité de prévision. Les modèles avec moins de termes sont également moins susceptibles d’inclure des termes redondants. Par exemple, les termes saisonniers autorégressifs sont parfois redondants avec les termes de moyenne mobile saisonnière. Les termes redondants rendent parfois les estimations des coefficients instables. Les conséquences de coefficients instables peuvent être les suivantes :

Les coefficients peuvent sembler non significatifs, même lorsqu'une relation significative existe entre le prédicteur et la réponse.
Les coefficients de prédicteurs fortement corrélés varieront considérablement d'un échantillon à un autre.
Lorsque des termes d'un modèle sont fortement corrélés, la suppression de l'un de ces termes aura une incidence considérable sur les coefficients estimés des autres. Les coefficients des termes fortement corrélés peuvent même présenter le mauvais signe.

* ATTENTION * Modèles ARIMA(p, d, q) inestimables qui n'incluent pas de terme constant :
(2; 1; 2)

Sélection du modèle

Modèle (d = 1)	LogVraisemblance	AICc	AIC	BIC
p = 0; q = 2*	-197,052	400,878	400,103	404,769
p = 1; q = 2	-196,989	403,311	401,978	408,199
p = 1; q = 0	-201,327	407,029	406,654	409,765
p = 2; q = 0	-200,239	407,251	406,477	411,143
p = 1; q = 1	-200,440	407,655	406,880	411,546
p = 2; q = 1	-201,776	412,884	411,551	417,773
p = 0; q = 1	-204,584	413,542	413,167	416,278
p = 0; q = 0	-213,614	429,350	429,229	430,784

Principaux résultats : AICc, BIC et AIC

L’ARIMA(0, 1, 2) a la meilleure valeur d’AICc. Les résultats ARIMA qui suivent concernent le modèle ARIMA(0, 1, 2). Si le modèle ne correspond pas suffisamment aux données, considérez d’autres modèles ayant des performances similaires, tels que le modèle ARIMA(1, 1, 2) et le modèle ARIMA (1, 1, 1). Si aucun des modèles ne correspond suffisamment aux données, demandez-vous s’il faut utiliser un autre type de modèle.

Etape 2 : Déterminer si chaque terme du modèle est significatif

Pour déterminer si l'association entre la réponse et chacun des termes du modèle est statistiquement significative, comparez la valeur de p du terme à votre seuil de signification pour évaluer l'hypothèse nulle. L’hypothèse nulle est que le terme n’est pas significativement différent de 0, ce qui indique qu’il n’existe aucune association entre le terme et la réponse. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un niveau de signification de 0,05 indique un risque de 5 % de conclure que le terme n’est pas significativement différent de 0 lorsqu’il est significativement différent de 0.

≤ α de la valeur P : Le terme est statistiquement significatif: Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez en conclure que le coefficient est statistiquement significatif.
> α de la valeur P : Le terme n’est pas statistiquement significatif: Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure que le coefficient est statistiquement significatif. Il est sans doute nécessaire de réajuster le modèle sans le terme.

Estimations finales des paramètres

Type	Coeff	Coef ErT	Valeur de T	Valeur de p
AR 1	-0,504	0,114	-4,42	0,000
Constante	150,415	0,325	463,34	0,000
Moyenne	100,000	0,216

Principaux résultats : P, Coef

Le terme autorégressif a une valeur de p inférieure au seuil de signification de 0,05. Vous pouvez en conclure que le coefficient du terme autorégressif est statistiquement significatif : vous devez conserver le terme dans le modèle.

Etape 3 : Déterminer si votre modèle respecte l'hypothèse de l'analyse

Utilisez les statistiques du Khi deux de Ljung-Box et la fonction d'autocorrélation des valeurs résiduelles pour déterminer si le modèle respecte les hypothèses selon lesquelles les valeurs résiduelles sont indépendantes. Si cette hypothèse n'est pas vérifiée, il se peut que le modèle ne soit pas ajusté aux données et vous devez être prudent lors de l'interprétation des résultats.

Statistiques du Khi deux de Ljung-Box: Pour déterminer si les valeurs résiduelles sont indépendantes, comparez la valeur de p au seuil de signification pour chaque statistique du Khi deux. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Si la valeur de p est supérieure au seuil de signification, vous pouvez en conclure que les valeurs résiduelles sont indépendantes et que le modèle respecte l'hypothèse.
Fonction d'autocorrélation des valeurs résiduelles: Si aucune corrélation significative n'est présente, vous pouvez en conclure que les valeurs résiduelles sont indépendantes. Toutefois, vous pouvez relever 1 ou 2 corrélations significatives pour des décalages d'ordre supérieur qui ne sont pas des décalages de saisonnalité. Ces corrélations sont en général dues à l'erreur aléatoire et ne signifient pas que l'hypothèse n'est pas respectée. Dans un tel cas, vous pouvez conclure que les valeurs résiduelles sont indépendantes.

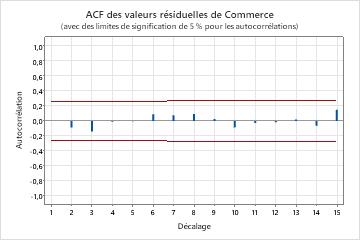
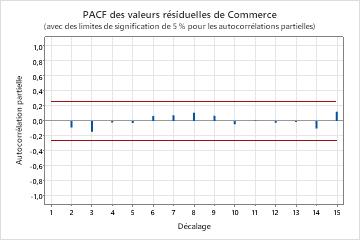
Résultats principaux : valeur de p, ACF des valeurs résiduelles
Dans ces résultats, les valeurs de p pour les statistiques du Khi deux de Ljung-Box sont supérieures à 0,05 et aucune des corrélations de la fonction d'autocorrélation des valeurs résiduelles n'est significative. Vous pouvez en conclure que le modèle respecte l'hypothèse selon laquelle les valeurs résiduelles sont indépendantes.

Décalage	12	24	36	48
Khi deux	4,05	12,13	25,62	32,09
DL	10	22	34	46
Valeur de p	0,945	0,955	0,849	0,940