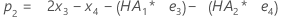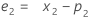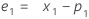Sur ce thème
Equation du modèle
Le lissage exponentiel double emploie une composante de niveau et une composante de tendance par période. Il utilise deux pondérations (également appelées paramètres de lissage) pour actualiser les composantes à chaque période. Les équations de lissage exponentiel double sont les suivantes :
Formule
Lt= αYt+ (1 – α) [Lt–1 + Tt–1]
Tt= γ [Lt – Lt–1] + (1 – γ) Tt–1
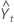 = Lt−1
+ Tt−1
= Lt−1
+ Tt−1
La première observation porte le numéro 1. Pour pouvoir poursuivre, les estimations de niveau et de tendance à l'instant zéro doivent ensuite être initialisées. La méthode d'initialisation utilisée pour déterminer les valeurs lissées peut être obtenue de deux façons : avec des pondérations optimales ou avec des pondérations que vous définissez.
Notation
| Terme | Description |
|---|---|
| Lt | niveau à l'instant t |
| α | pondération pour le niveau |
| Tt | Tendance à l'instant t |
| γ | pondération pour la tendance |
| Yt | valeur de données à l'instant t |
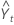 | valeur prévue pour l'instant t |
Pondérations
Pondérations ARIMA optimisées
- Minitab ajuste un modèle ARIMA (0,2,2) aux données afin de minimiser la somme du carré des erreurs.
- Les composantes de niveau et de tendance sont ensuite initialisées par extrapolation rétrospective.
Pondérations spécifiées
- Minitab ajuste un modèle de régression linéaire aux données de séries chronologiques (variable y) en fonction du temps (variable x).
- La constante de cette régression est l'estimation initiale de la composante de niveau, tandis que le coefficient de pente est l'estimation initiale de la composante de tendance.
Si vous spécifiez des pondérations qui correspondent à un modèle ARIMA (0,2,2) à racines égales, la méthode de Holt se rapproche de la méthode de Brown1.
Méthode de calcul des valeurs initiales pour le niveau et la tendance
peut stocker des estimations pour le niveau et la tendance. Minitab utilise une des méthodes suivantes pour calculer les valeurs de la première ligne de ces colonnes, selon les options que vous spécifiez dans la boîte de dialogue.
Si vous choisissez l’option ARIMA optimal dans Lissage exponentiel double, Minitab utilise la méthode suivante pour calculer les premières valeurs de niveau et de tendance. Vous pouvez effectuer ces étapes à la main.
- Choisissez pour calculer les valeurs de pondération optimale par ARIMA. Configurez la boîte de dialogue comme suit :
- Dans la zone Autorégressif, saisissez 0.
- Dans la zone Différence, saisissez 2.
- Dans la zone Moyenne mobile, saisissez 2.
- Décochez la case Inclure un terme constant dans le modèle.
- Cliquez sur Stockage, puis cochez Valeurs résiduelles. Cliquez sur OK dans chaque boîte de dialogue
- Minitab utilise les valeurs MA de la sortie ARIMA
pour calculer les pondérations optimales comme suit :

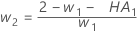
- Minitab calcule ensuite à l'envers pour revenir à l'observation initiale, en utilisant les données d’observations ultérieures :
où :
Terme Description pi la valeur prévue de la ie observation lissée xi la valeur de la ie observation dans la série chronologique ei la valeur du ie résidu, stocké depuis ARIMA ci-dessus -
- Minitab calcule la valeur initiale pour le niveau (L1) :

- Minitab calcule la valeur initiale pour la tendance (T1) :
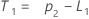
- Créez une colonne d’indices de temps de même longueur que votre colonne de données de série chronologique. Une colonne d’entiers de 1 à n suffit.
- Sélectionnez .
- Dans Réponses, entrez la colonne de données de série chronologique. Dans Prédicteurs continus, entrez la colonne d'indices de temps.
- Cliquez sur Stockage, puis cochez Coefficients. Cliquez sur OK dans chaque boîte de dialogue
- La valeur initiale pour le niveau est :
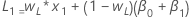
- La valeur initiale pour la tendance est :
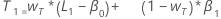 où :
où :Terme Description L1 valeur initiale pour le niveau x1 valeur de la première observation dans la série chronologique T1 valeur initiale pour la tendance wL valeur de pondération pour le niveau wT valeur de pondération pour la tendance β0 coefficient du terme constant dans le modèle de régression β1 coefficient du terme prédicteur dans le modèle de régression
Prévisions
Le lissage exponentiel double utilise les composantes de tendance et de niveau pour générer des prévisions. La prévision pour un point à l'instant t à m périodes dans le futur est déterminée comme suit :
Formule
Lt + mTt
Les données allant jusqu'à l'instant d'origine de la prévision sont utilisées pour le lissage.
Notation
| Terme | Description |
|---|---|
| Lt | niveau à l'instant t |
| Tt | tendance à l'instant t |
Limites de prévision
Formule
- Limite supérieure = Prévision + 1,96 × dt × MAD
- Limite inférieure = Prévision – 1,96 × dt × MAD
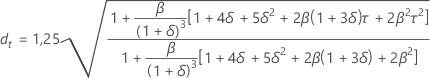
Notation
| Terme | Description |
|---|---|
| β | max{α, γ) |
| δ | 1 – β |
| α | constante de lissage de niveau |
| γ | constante de lissage de tendance |
| τ |  |
| b0(T) | 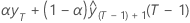 |
| b1(T) | 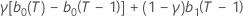 |
MAPE
La valeur MAPE (pourcentage d'erreur absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude sous forme de pourcentage.
Formule
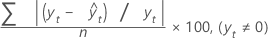
Notation
| Terme | Description |
|---|---|
| yt | valeur réelle à l'instant t |
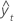 | valeur ajustée |
| n | nombre d'observations |
MAD
La valeur MAD (écart absolu moyen) mesure l'exactitude des valeurs de la série chronologique ajustée. Elle exprime l'exactitude dans les mêmes unités que les données, ce qui aide à conceptualiser l'importance de l'erreur.
Formule
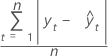
Notation
| Terme | Description |
|---|---|
| yt | valeur réelle à l'instant t |
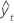 | valeur ajustée |
| n | nombre d'observations |
MSD
La valeur MSD (écart quadratique moyen) est toujours calculée à l'aide du même dénominateur, n, indifféremment du modèle. Par rapport à MAD, la mesure MSD est une mesure plus sensible des erreurs de prévision inhabituellement élevées.
Formule
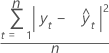
Notation
| Terme | Description |
|---|---|
| yt | valeur réelle à l'instant t |
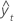 | valeur ajustée |
| n | nombre d'observations |