Décalage
Le décalage est le nombre de périodes qui séparent les deux séries chronologiques. Par défaut, le nombre de décalages est compris entre (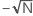
+ 10) et (
+ 10).
Fonction d'intercorrélation (CCF)
La fonction d'intercorrélation représente la corrélation entre les observations de deux séries chronologiques xt et yt, séparées par k unités de temps (la corrélation entre yt+k et xt).
Interprétation
La fonction d'intercorrélation permet de déterminer s'il existe une relation entre deux séries chronologiques. Pour déterminer s'il existe une relation entre deux séries chronologiques, recherchez une importante corrélation, où les corrélations de chaque côté deviennent rapidement non significatives. En général, une corrélation est significative lorsque la valeur absolue est supérieure à 
, où n est le nombre d'observations et k est le décalage. Ce calcul est une procédure empirique fondée sur une approximation selon la loi normale pour grands échantillons. Si l'intercorrélation de population de décalage k a pour valeur zéro lorsque k = 1, 2, ..., alors, pour une valeur élevée de n, rxy(k) sera approximativement normalement distribué, avec une moyenne (μ) de zéro et un écart type (σ) de 1/
. Dans la mesure où environ 95 % d'une population normale se situe à moins de 2 écarts types de la moyenne, un test qui rejette l'hypothèse selon laquelle l'intercorrélation de population de décalage k est égale à zéro lorsque | rxy(k) | est supérieur à 2/
a un seuil de signification (α) d'environ 5 %.
Remarque
L'interprétation de la fonction d'intercorrélation dépend de l'hypothèse selon laquelle il n'existe pas d'autocorrélation. Pour plus d'informations, reportez-vous à la rubrique Rechercher une preuve d'autocorrélation.
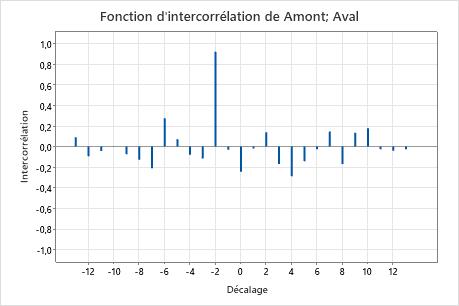
Su ce diagramme, la corrélation au niveau du décalage -2 est d'environ 0,92. Etant donné que 0,92 > 0,5547 = 
, la corrélation est significative. Vous pouvez en conclure que l'eau met deux jours à s'écouler de l'emplacement en amont vers celui en aval.
