Un analyste a recueilli des données sur le nombre de passagers aériens pendant 108 mois. L’analyste souhaite utiliser un modèle ARIMA pour générer des prévisions pour les données. Sur un graphique de série chronologique, l’analyste constate que la différence entre les pics saisonniers élevés et bas augmente avec le temps. Ce modèle indique que la variance n’est pas stationnaire. L’analyste effectue une transformation de Box-Cox pour rendre la variance stationnaire avant qu’il n’adapte le modèle ARIMA.
- Ouvrez l’exemple de données PassagersAeriens.MWX.
- Sélectionnez .
- Dans Série, saisissez Nombre de passagers.
- Dans Période saisonnière, entrez 12.
- Sélectionnez λ optimal cette option pour que Minitab Statistical Software recherche une transformation à utiliser.
- Dans Colonne d'étiquette pour l'échelle de temps, saisissez Date.
- Dans Stocker la série transformée dans, saisissez Transformé. Cliquez sur OK.
Interprétation des résultats
Le tableau Méthode indique les paramètres de l’analyse et la valeur de λ pour la transformation.
Dans ces résultats, la période saisonnière est de 12 et l’analyse recherche une valeur λ entre la plage par défaut de -1 et 2. La valeur optimale pour λ est d’environ -0,14. L’analyse arrondit la valeur à 0 et utilise la transformation logarithmique naturelle.
Méthode
| Période saisonnière | 12 |
|---|---|
| Sélectionner le λ optimal dans l'intervalle | [-1; 2] |
| λ optimal | -0,144439 |
| λ arrondi optimal | 0 |
| Série transformée = ln(Nombre de passagers) |
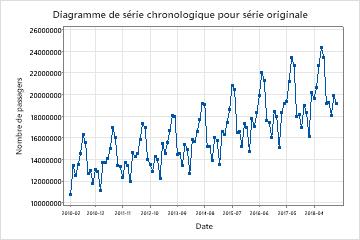
Comparez la série chronologique de la série originale au diagramme de série chronologique de la série transformée pour vérifier que la transformation rend la variance stationnaire.
Dans ces résultats, le diagramme de série chronologique de la série originale montre la variance non stationnaire. Dans ces données, la différence entre les points hauts et les points bas d’un cycle saisonnier augmente avec le temps. Ce modèle montre que la variance augmente avec le temps.
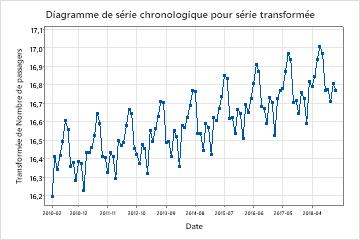
Examinez le diagramme de série chronologique de la série transformée pour vérifier que la transformation rend la variance stationnaire.
Dans ces résultats, le graphique des séries chronologiques des séries transformées montre une différence approximativement égale entre les points hauts et les points bas des cycles saisonniers. Ce modèle montre que la transformation rend la variance stationnaire.
Examinez également le diagramme de séries chronologiques des données transformées pour évaluer d’autres caractéristiques importantes des séries transformées. Par exemple, les hypothèses d’un modèle ARIMA incluent que la série a une moyenne stationnaire en plus d’une variance stationnaire. Si un diagramme de série chronologique de la série transformée montre que la série transformée n’a pas de moyenne stationnaire, essayez de Test augmenté de Dickey-Fuller voir si la différenciation des données rend la moyenne de la série stationnaire.
Dans ces résultats, la série transformée montre une tendance à la hausse. Ce schéma montre que la moyenne de la série n’est pas stationnaire. Utilisez la Test augmenté de Dickey-Fuller colonne stockée des données transformées pour déterminer si la différenciation rend la série stationnaire.