La fonction d'autocorrélation est une mesure de la corrélation entre des observations d'une série chronologique séparées par k unités de temps (yt et yt–k).
Interprétation
Utilisez les fonctions d'autocorrélation partielle et d'autocorrélation conjointement pour déterminer des modèles ARIMA. Etudiez les pics au niveau de chaque décalage pour déterminer s'ils sont significatifs. Un pic significatif dépasse les limites de signification, ce qui indique que la corrélation correspondant à ce décalage n'est pas égale à zéro.
Remarque
Les données doivent être stationnaires pour que vous puissiez interpréter le diagramme d'autocorrélation. Une série chronologique stationnaire possède une moyenne, une variance et une fonction d'autocorrélation plus ou moins constantes dans le temps. Pour plus d'informations, consultez la rubrique Observations relatives aux données pour la fonction d'autocorrélation.
| Schéma | Interprétation du schéma | Exemple |
|---|---|---|
| Pic important au niveau du décalage 1 qui diminue après quelques décalages. | Terme autorégressif dans les données. Utilisez la fonction d'autocorrélation partielle pour déterminer l'ordre du terme autorégressif. | 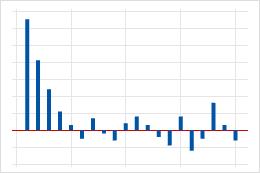 |
| Pic important au niveau du décalage 1, suivi par un motif en vague décroissant qui alterne entre corrélations positive et négative. | Terme autorégressif d'ordre supérieur dans les données. Utilisez la fonction d'autocorrélation partielle pour déterminer l'ordre du terme autorégressif. | 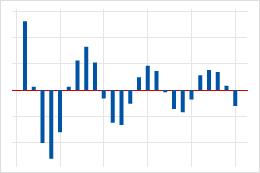 |
| Corrélations significatives au niveau du premier ou du deuxième décalage, suivies de corrélations non significatives. | Terme de moyenne mobile dans les données. Le nombre de corrélations significatives indique l'ordre du terme de moyenne mobile. | 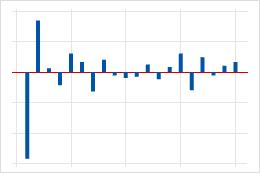 |
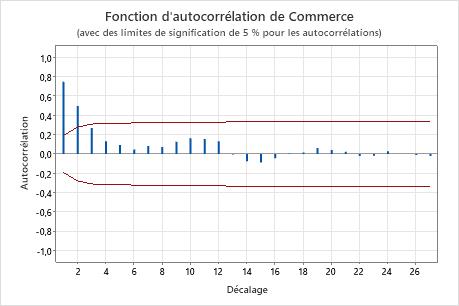
Sur ce diagramme, il existe une corrélation significative au niveau du décalage 1 qui diminue après quelques décalages. Ce schéma indique la présence d'un terme autorégressif. Vous devez utiliser la fonction d'autocorrélation partielle pour déterminer l'ordre de ce terme.
