Modèles de régression
| Terme | Description |
|---|---|
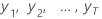 | les valeurs des séries chronologiques observées dans le temps = 1, ..., T |
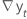 | la différence de deux observations consécutives au temps t, 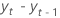 , où t = 2, ..., T , où t = 2, ..., T |
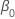 | le terme constant dans un modèle de régression |
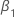 | le coefficient d’une tendance temporelle linéaire dans un modèle de régression |
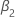 | le coefficient d’une tendance temporelle quadratique dans un modèle de régression |
 | l’ordre de décalage du processus autorégressif |
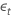 | le terme d’erreur indépendant en série au temps t pour t = 2, ..., T |
- Un modèle avec seulement un coefficient constant

- Un modèle avec un coefficient constant et un coefficient linéaire
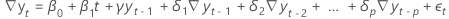
- Un modèle avec un coefficient constant, un coefficient linéaire et un coefficient quadratique

- Un modèle sans coefficients de régression
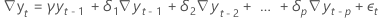
Hypothèses
Chaque test augmenté de Dickey-Fuller utilise les hypothèses suivantes :
Hypothèse nulle, H0: 
Hypothèse alternative, H1: 
L’hypothèse nulle dit qu’une racine unitaire se trouve dans l’échantillon de série chronologique, ce qui signifie que la moyenne des données n’est pas stationnaire. Le rejet de l’hypothèse nulle indique que la moyenne des données est stationnaire ou stationnaire de tendance, selon le modèle du test.
Statistique de test

où
| Terme | Description |
|---|---|
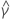 | l’estimation du coefficient le moins carré de l' 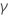 coefficient coefficient |
 | l’erreur-type de l’estimation des moindres carrés de l' 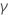 coefficient du modèle de régression coefficient du modèle de régression |
Valeurs p approximatives de MacKinnon
Dans l’hypothèse nulle, la distribution asymptotique de la statistique de test ne suit pas une loi standard. Fuller (1976)1 provides a table with common percentiles of the asymptotic distribution. MacKinnon (19942, 20103) applique des approximations de surface de réponse aux données simulées afin de fournir une valeur p approximative pour toute valeur de la statistique de test ADF.
Si les spécifications de l’analyse utilisent 0,01, 0,05 ou 0,1 comme niveau de signification, l’évaluation de l’hypothèse nulle compare la statistique de test à la valeur critique pour ce niveau de signification. Si la statistique de test est inférieure ou égale à la valeur critique, rejetez l’hypothèse nulle.
Si les spécifications de l’analyse donnent un niveau de signification différent, alors l’évaluation de l’hypothèse nulle compare la valeur approximative de p au niveau de signification. Si la valeur de p est inférieure au niveau de signification, rejetez l’hypothèse nulle.
Valeurs critiques pour les niveaux de signification 0,01, 0,05 et 0,1
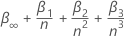
où n est le nombre d’observations que l’analyse utilise pour s’adapter au modèle de régression. Les valeurs pour 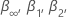 et
et 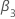 proviennent des tables de MacKinnon (2010). Si la statistique de test est inférieure ou égale à la valeur critique, rejetez l’hypothèse nulle.
proviennent des tables de MacKinnon (2010). Si la statistique de test est inférieure ou égale à la valeur critique, rejetez l’hypothèse nulle.
Valeurs p approximatives
Le calcul de la valeur approximative de p provient de Mackinnon (1994). Comparez la valeur de p au niveau de signification pour prendre une décision. Si la valeur de p est inférieure ou égale au niveau de signification, rejetez l’hypothèse nulle.
Détermination de l’ordre de décalage

Le choix de l’ordre de décalage dépend du critère dans les spécifications de l’analyse. Si les spécifications de l’analyse n’incluent pas de critère, alors le modèle de régression pour le test est l’ordre maximal de p.
Dans les calculs pour déterminer l’ordre de décalage, le nombre d’observations dépend de l’ordre de décalage maximal tel que m = n – p – 1.
| Terme | Description |
|---|---|
| n | nombre total d'observations |
| p | l’ordre de décalage maximal des termes différents qui se trouvent dans le modèle |
Le calcul de chaque critère suit :
Critère d'information d'Akaike (AIC)
L’analyse évalue un modèle de régression pour chaque ordre de décalage dans les spécifications de l’analyse. L’ordre de décalage pour le test est le modèle de régression avec la valeur minimale de l’AIC.
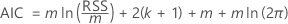
où
| Terme | Description |
|---|---|
| m | le nombre d’observations qui dépend de l’ordre de décalage maximal |
| k | le nombre de coefficients dans le modèle, y compris la constante si le modèle de régression a une constante non nulle |
| RSS | la somme résiduelle des carrés du modèle de régression |
Critère d’information Bayésien (BIC)
L’analyse évalue un modèle de régression pour chaque ordre de décalage dans les spécifications de l’analyse. L’ordre de décalage pour le test est le modèle de régression avec la valeur minimale de l’BIC.
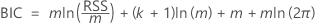
où
| Terme | Description |
|---|---|
| m | le nombre d’observations qui dépend de l’ordre de décalage maximal |
| k | le nombre de coefficients dans le modèle, y compris la constante si le modèle de régression a une constante non nulle |
| RSS | la somme résiduelle des carrés du modèle de régression |
statistique t
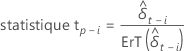
où i = 1, ..., p
| Terme | Description |
|---|---|
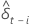 | l’estimation des moindres carrés de l'  coefficient dans le modèle de régression coefficient dans le modèle de régression |
 | l’erreur-type de l’estimation des moindres carrés de l'  coefficient dans le modèle de régression coefficient dans le modèle de régression |
