Etape 1 : Déterminer si les données sont stationnaires ou stationnaires de tendance
Le tableau du test de augmenté Dickey-Fuller fournit les hypothèses, une statistique de test, une valeur de p et une recommandation sur l’opportunité de prendre en compte la différenciation non saisonnière pour rendre les données stationnaires.
La statistique de test fournit un moyen d’évaluer l’hypothèse nulle. Les statistiques de test qui sont inférieures ou égales à la valeur critique fournissent des preuves contre l’hypothèse nulle.
La valeur de p est une probabilité qui mesure la preuve par rapport à l’hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Pour déterminer s’il faut différencier les données, comparez la statistique de test à la valeur critique ou la valeur p à votre niveau de signification. Étant donné que la valeur de p contient plus d’approximation, la recommandation de l’analyse utilise la valeur critique pour évaluer l’hypothèse nulle lorsque le niveau de signification est de 0,01, 0,05 ou 0,10. Habituellement, la conclusion est la même pour la valeur critique et la valeur p. L’hypothèse nulle est que les données ne sont pas stationnaires, ce qui implique que la différenciation est une étape raisonnable pour essayer de rendre les données stationnaires.
- Valeur P ≤ niveau de signification
- Statistiques de test ≤ valeur critique
- Si la valeur de p est inférieure ou égale au niveau de signification ou si la statistique de test est inférieure ou égale à la valeur critique, la décision est de rejeter l’hypothèse nulle. Étant donné que les données fournissent la preuve que les données sont stationnaires, la recommandation de l’analyse est de procéder sans différenciation.
- Valeur P > niveau de signification
- Statistiques de test > valeur critique
- Si la valeur de p est supérieure au niveau de signification ou si la statistique de test est supérieure à la valeur critique, la décision est de ne pas rejeter l’hypothèse nulle. Étant donné que les données ne fournissent pas la preuve que les données sont stationnaires, la recommandation de l’analyse est de déterminer si la différenciation rend la moyenne des données stationnaire.
Si les données sont stationnaires, le test ne recommande pas de différenciation. Explorez les modèles ARIMA qui n’incluent aucun terme de différenciation. Si les données ne sont pas stationnaires, explorez les modèles ARIMA qui incluent des termes différents. Utilisez le diagramme de série chronologique des données différentielles pour voir si les différences entre les observations consécutives sont un ensemble de données stationnaires. Si les données divergentes sont stationnaires, il est raisonnable de considérer les modèles ARIMA avec un terme de premier ordre pour la différenciation.
Dans ces résultats, la statistique de test de 2,29045 est supérieure à la valeur critique d’environ -2,96053. Étant donné que les résultats ne rejettent pas l’hypothèse nulle selon laquelle les données ne sont pas stationnaires, la recommandation du test est d’envisager une différenciation pour rendre les données stationnaires.
Test augmenté de Dickey-Fuller
| Hypothèse nulle : | Les données ne sont pas stationnaires |
|---|---|
| Hypothèse alternative : | Les données sont stationnaires |
| Statistique du test | Valeur de P |
|---|---|
| 2,29045 | 0,999 |
| Statistique du test | Recommandation |
|---|---|
| 2,29045 | Statistique de test > valeur critique de -2,96053. |
| Seuil de signification = 0,05 | |
| Echec du rejet de l'hypothèse nulle. | |
| Envisagez de faire une différenciation pour rendre les données stationnaires. |
Etape 2 : Examiner l’effet de la différenciation des données
Lorsque la conclusion de l’essai permet de différencier, examiner les graphiques des données différenciées pour les caractéristiques des données qui ne sont pas stationnaires. Une tendance dans le diagramme de série chronologique est un exemple de modèle qui indique que la moyenne des données n’est pas stationnaire. Sur le diagramme ACF, de gros pics qui diminuent lentement indiquent également des données qui ne sont pas stationnaires. Si vous voyez ces modèles dans les données différenciées, demandez-vous s’il faut adapter un modèle ARIMA avec un deuxième ordre de différenciation. Habituellement, 1 ou 2 ordres de différenciation suffisent pour fournir un ajustement raisonnable aux données.
Si les données différenciées sont stationnaires, une approche raisonnable consiste à inclure un seul ordre de différenciation non saisonnière dans un modèle ARIMA. Pour plus d’informations sur les modèles ARIMA, reportez-vous à la ARIMA - Généralités section.
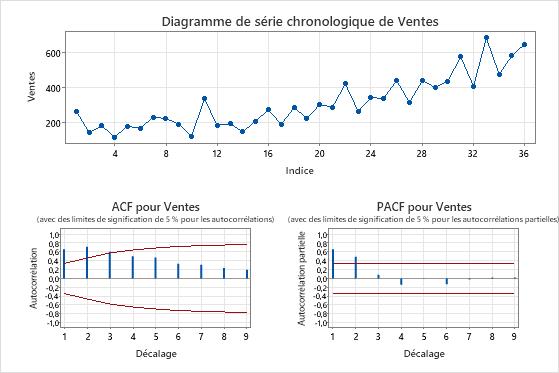
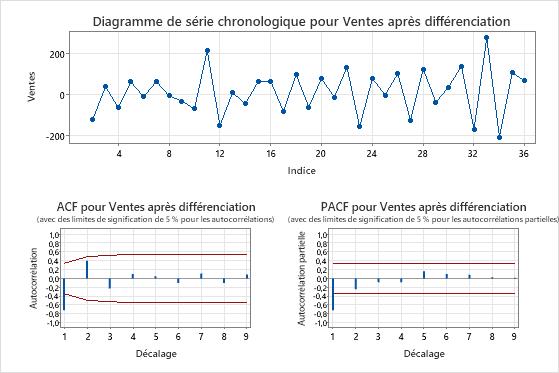
Les graphiques des séries chronologiques montrent le résultat de la différenciation. Dans ces résultats, le graphique des séries chronologiques des données originales montre une tendance claire. Le graphique de série chronologique des données différenciées montre les différences entre les valeurs consécutives. Les données différenciées semblent stationnaires car les points suivent un chemin horizontal sans motifs évidents dans la variation.
Les graphiques ACF montrent également l’effet de la différenciation. Dans ces résultats, le diagramme ACF des données originales montre une diminution lente des pics à travers les décalages. Ce modèle indique que les données ne sont pas stationnaires. Dans le diagramme ACF des données différenciées, le seul pic significativement différent de 0 est au décalage 1.
Dans ces résultats, les graphiques de séries chronologiques et les graphiques ACF confirment les résultats des tests. Par conséquent, une approche raisonnable consiste à différencier les données, puis à adapter un modèle autorégressif et de moyenne mobile pour faire des prévisions.