Sur ce thème
Tableau de méthode
Le tableau Méthode affiche les paramètres de l’analyse et l’ordre de décalage sélectionné.
Dans ces résultats, l’ordre de décalage maximal évalué par l’analyse est de 9. L’analyse utilise le modèle avec l’ordre de décalage le plus élevé de 4 pour calculer les résultats des tests.
Méthode
| Ordre de décalage maximal pour les termes dans le modèle de régression | 9 |
|---|---|
| Critère de sélection de l'ordre de décalage | AIC minimal |
| Termes supplémentaires | Constante |
| Ordre de décalage sélectionné | 4 |
| Lignes utilisées | 36 |
Table de test augmenté de Dickey-Fuller
Le tableau de test augmenté de Dickey-Fuller fournit les hypothèses, une statistique de test, une valeur de p et une recommandation sur l’opportunité d’envisager une différenciation pour rendre la série stationnaire.
La statistique de test fournit un moyen d’évaluer l’hypothèse nulle. Les statistiques de test qui sont inférieures ou égales à la valeur critique fournissent des preuves contre l’hypothèse nulle.
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Pour déterminer s’il faut différencier les données, comparez la statistique de test à la valeur critique ou la valeur p à votre niveau de signification. Étant donné que la valeur de p contient plus d’approximation, la recommandation de l’analyse utilise la valeur critique pour évaluer l’hypothèse nulle lorsque le niveau de signification est de 0,01, 0,05 ou 0,10. Habituellement, la conclusion est la même pour la valeur critique et la valeur p. L’hypothèse nulle est que les données ne sont pas stationnaires, ce qui implique que la différenciation est une étape raisonnable pour essayer de rendre les données stationnaires.
- Valeur P ≤ niveau de signification
- Statistiques de test ≤ valeur critique
- Si la valeur de p est inférieure ou égale au niveau de signification ou si la statistique de test est inférieure ou égale à la valeur critique, la décision est de rejeter l’hypothèse nulle. Étant donné que les données fournissent la preuve que les données sont stationnaires, la recommandation de l’analyse est de procéder sans différenciation.
- Valeur P > niveau de signification
- Statistiques de test > valeur critique
- Si la valeur de p est supérieure au niveau de signification ou si la statistique de test est supérieure à la valeur critique, la décision est de ne pas rejeter l’hypothèse nulle. Étant donné que les données ne fournissent pas la preuve que les données sont stationnaires, la recommandation de l’analyse est de déterminer si la différenciation rend la moyenne des données stationnaire.
Dans ces résultats, la statistique de test de 2,29045 est supérieure à la valeur critique d’environ -2,96053. Étant donné que les résultats ne rejettent pas l’hypothèse nulle selon laquelle les données ne sont pas stationnaires, la recommandation du test est d’envisager une différenciation pour rendre les données stationnaires.
Test augmenté de Dickey-Fuller
| Hypothèse nulle : | Les données ne sont pas stationnaires |
|---|---|
| Hypothèse alternative : | Les données sont stationnaires |
| Statistique du test | Valeur de P |
|---|---|
| 2,29045 | 0,999 |
| Statistique du test | Recommandation |
|---|---|
| 2,29045 | Statistique de test > valeur critique de -2,96053. |
| Seuil de signification = 0,05 | |
| Echec du rejet de l'hypothèse nulle. | |
| Envisagez de faire une différenciation pour rendre les données stationnaires. |
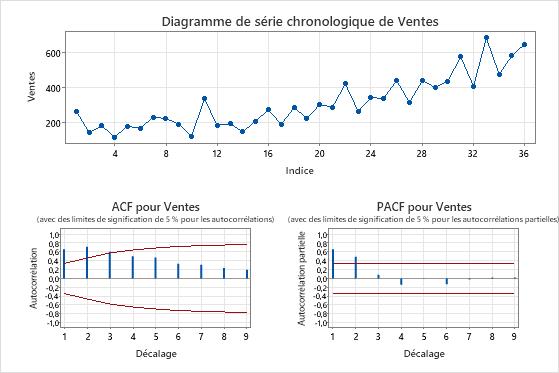
Diagrammes de la série originale
- Diagramme de série chronologique
- Utilisez le diagramme de série chronologique de la série originale pour examiner les caractéristiques des données originales. Une tendance est un exemple de modèle qui indique une moyenne non stationnaire. Utilisez la différenciation pour essayer de rendre la moyenne stationnaire.
- Diagramme ACF
- Utilisez la fonction d’autocorrélation (ACF) des données d’origine pour rechercher un modèle qui indique que la moyenne des données n’est pas stationnaire. Un schéma commun est de grands pics à travers les décalages qui s’éteignent très lentement.
- Diagramme PACF
- Habituellement, vous utilisez la fonction d’autocorrélation partielle (PACF) des données stationnaires pour rechercher des modèles qui indiquent la présence de termes autorégressifs dans un modèle ARIMA. Si les données d’origine ne sont pas stationnaires, utilisez le diagramme PACF de la série différenciée pour rechercher des termes candidats pour le modèle ARIMA.
Dans ces résultats, les données montrent une tendance à la hausse sur le graphique des séries chronologiques. Le premier décalage sur le diagramme ACF montre un pic important qui dépasse la limite de signification de 5%, puis diminue très lentement. Ces modèles indiquent que la moyenne des données n’est pas stationnaire.
Étant donné que les ventes n’ont aucune relation avec un prédicteur qui expliquerait une tendance déterministe et que l’analyste souhaite utiliser un modèle ARIMA pour prévoir les ventes, différencier les données est un moyen raisonnable d’essayer de rendre la moyenne de la série stationnaire.
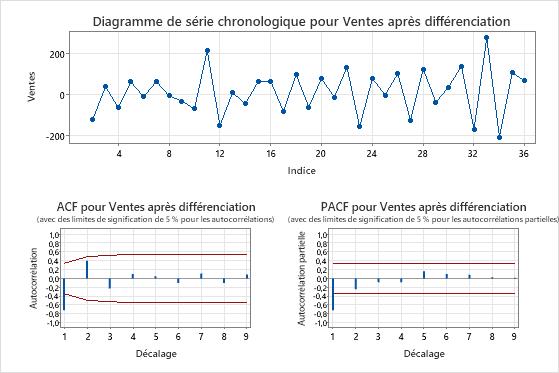
Diagrammes des séries différenciées
- Graphique de série chronologique après différenciation
- Utilisez le diagramme de série chronologique des données différentes pour vérifier que la différenciation rend la moyenne des données stationnaire. Le graphique de la série chronologique montre les différences entre les observations consécutives. Les données avec une moyenne stationnaire suivent un chemin horizontal sur le diagramme de série chronologique.
- Diagramme ACF et Diagramme PACF après différenciation
- Utilisez l’ACF des données différenciées pour vérifier que la différenciation rend la moyenne des données stationnaire. Les graphiques avec des pics qui diminuent rapidement sont caractéristiques des données stationnaires.
Dans ces résultats, le graphique de la série chronologique montre que la moyenne et la variance des données différentielles sont approximativement constantes. Les données semblent être stationnaires.
Dans le diagramme ACF des données différenciées, le seul pic significativement différent de 0 est au décalage 1. Cette tendance suggère également que les données sont stationnaires.