Sur ce thème
Etape 1 : Déterminer si chaque terme dans le modèle est significatif
- Valeur de p ≤ α : le terme est statistiquement significatif
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez en conclure que le coefficient est statistiquement significatif.
- Valeur de p > α : le terme n'est pas statistiquement significatif
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure que le coefficient est statistiquement significatif. Il est sans doute nécessaire de réajuster le modèle sans le terme.
Estimations finales des paramètres
| Type | Coeff | Coef ErT | Valeur de T | Valeur de p |
|---|---|---|---|---|
| AR 1 | -0,504 | 0,114 | -4,42 | 0,000 |
| Constante | 150,415 | 0,325 | 463,34 | 0,000 |
| Moyenne | 100,000 | 0,216 |
Résultats principaux : P, Coeff
Le terme autorégressif a une valeur de p inférieure au seuil de signification de 0,05. Vous pouvez en conclure que le coefficient du terme autorégressif est statistiquement significatif : vous devez conserver le terme dans le modèle.
Etape 2 : Déterminer l'ajustement du modèle aux données
Utilisez le carré moyen de l'erreur (CM) pour déterminer le degré d'ajustement du modèle aux données. Plus les valeurs sont basses, meilleur est l'ajustement du modèle.
Somme des carrés des valeurs résiduelles
| DL | Somme des carrés | CM |
|---|---|---|
| 58 | 366,733 | 6,32299 |
Résultats principaux : CM
Le carré moyen de l'erreur est de 6,323 pour ce modèle. Cette valeur n'offre pas beaucoup d'informations en elle-même, mais elle permet de comparer l'ajustement de différents modèles ARIMA.
Etape 3 : Déterminer si votre modèle respecte l'hypothèse de l'analyse
- Statistiques du Khi deux de Ljung-Box
- Pour déterminer si les valeurs résiduelles sont indépendantes, comparez la valeur de p au seuil de signification pour chaque statistique du Khi deux. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Si la valeur de p est supérieure au seuil de signification, vous pouvez en conclure que les valeurs résiduelles sont indépendantes et que le modèle respecte l'hypothèse.
- Fonction d'autocorrélation des valeurs résiduelles
- Si aucune corrélation significative n'est présente, vous pouvez en conclure que les valeurs résiduelles sont indépendantes. Toutefois, vous pouvez relever 1 ou 2 corrélations significatives pour des décalages d'ordre supérieur qui ne sont pas des décalages de saisonnalité. Ces corrélations sont en général dues à l'erreur aléatoire et ne signifient pas que l'hypothèse n'est pas respectée. Dans un tel cas, vous pouvez conclure que les valeurs résiduelles sont indépendantes.
Box-Pierce (Ljung-Box) modifiée Statistique du Khi deux
| Décalage | 12 | 24 | 36 | 48 |
|---|---|---|---|---|
| Khi deux | 4,05 | 12,13 | 25,62 | 32,09 |
| DL | 10 | 22 | 34 | 46 |
| Valeur de p | 0,945 | 0,955 | 0,849 | 0,940 |
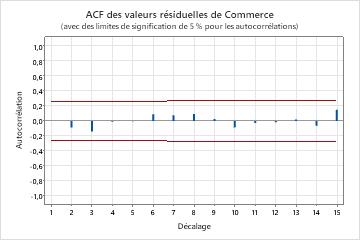
Résultats principaux : valeur de p, ACF des valeurs résiduelles
Dans ces résultats, les valeurs de p pour les statistiques du Khi deux de Ljung-Box sont supérieures à 0,05 et aucune des corrélations de la fonction d'autocorrélation des valeurs résiduelles n'est significative. Vous pouvez en conclure que le modèle respecte l'hypothèse selon laquelle les valeurs résiduelles sont indépendantes.
