Utilisations de la loi log-normale pour modéliser les données de fiabilité
La loi log-normale est une loi flexible étroitement liée à la loi normale. Cette loi peut s'avérer particulièrement utile pour la modélisation de données à peu près symétriques ou asymétriques vers la droite. A l'instar de la loi de Weibull, la loi log-normale peut paraître sensiblement différente selon son paramètre d'échelle.
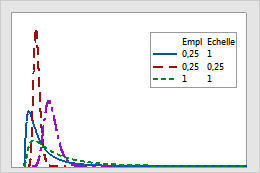
En fait, le modèle log-normal et le modèle de Weibull peuvent parfois s'ajuster à un ensemble spécifique de données de test de durée de vie aussi bien l'un que l'autre. Toutefois, vous devez tenir compte d'une différence importante. Lorsque vous utilisez ces lois pour extrapoler la plage de données échantillons, la loi log-normale prévoit des taux de défaillance moyens inférieurs plus tôt que la loi de Weibull.
- Défaillance due à des dégradations ou réactions chimiques : corrosion, migration ou diffusion, ce qui est courant dans le cas des défaillances de semi-conducteurs
- Délai avant fracture en cas de métaux soumis à la croissance de fissures
- Composants électroniques présentant un risque inférieur de défaillance au bout d'un certain temps
Exemple 1 : Composants électroniques
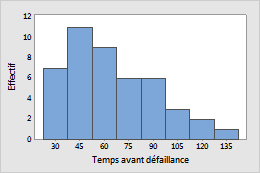
Des ingénieurs enregistrent le temps avant défaillance d'un composant électronique dans des conditions de fonctionnement normal. Le composant présente un risque inférieur de défaillance dans le temps, qui peut être modélisé à l'aide d'une loi log-normale.
Exemple 2 : Ventilateurs d'un groupe électrogène diesel
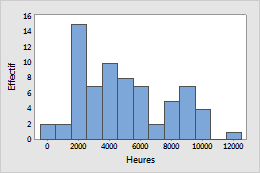
Le temps avant défaillance a été suivi pendant la durée de vie des ventilateurs d'un groupe électrogène diesel. Une loi log-normale a été utilisée pour modéliser les données.
Fonction de densité de probabilité et fonction de risque pour la loi log-normale
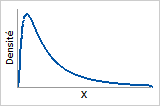
Fonction de densité de probabilité
Les données sont asymétriques vers la droite.
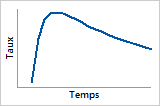
Fonction de risque
Le risque de défaillance augmente rapidement jusqu'à un maximum, puis diminue.
