Utilisations de la loi exponentielle pour modéliser les données de fiabilité
La loi exponentielle est une loi simple ayant un seul paramètre et généralement utilisée pour modéliser des données de fiabilité. La loi exponentielle est en fait un cas particulier de la loi de Weibull où ß = 1.
- La loi exponentielle est souvent utilisée pour modéliser des composants électroniques qui, en général, ne s'usent pas durant toute la durée de vie du produit dans lequel ils sont installés, et bien au-delà. Il s'agit par exemple de composants de circuits intégrés de haute qualité comme des diodes, des transistors, des résistances et des condensateurs.
- La loi exponentielle est également considérée comme un excellent modèle pour la longue période "plate" (relativement constante) de risque de défaillance faible qui caractérise la partie intermédiaire de la courbe "en baignoire". Cette phase correspond à la durée de vie utile du produit. Elle correspond à la partie "défaillance intrinsèque" de la courbe.
- Toutefois, la loi exponentielle ne doit pas être utilisée pour modéliser les composants mécaniques ou électriques censés montrer une fatigue, une corrosion ou une usure avant la fin de la durée de vie prévue du produit, comme les roulements à billes, ou certains lasers ou filaments.
La loi exponentielle se caractérise essentiellement par son absence de mémoire. Cette absence de mémoire indique que la durée de vie restante d'un composant ne dépend pas de l'âge qu'il a actuellement. Par exemple, un système qui fait l'objet d'une usure normale et qui présente de ce fait plus de risques de défaillances par la suite n'est pas sans mémoire. Par conséquent, cette loi doit être utilisée lorsque le taux de défaillance est constant pendant toute la durée de vie du produit. Le nombre de défaillances par unité dans le temps est généralement exprimé en pourcentage de défaillances par unité temporelle, tel que le pourcentage de défaillances par tranches de mille heures.
Exemple 1 : Transistors
Un composant électronique a un taux de défaillance que l'on sait constant durant la durée de vie prévue d'un produit. Des ingénieurs relèvent le temps avant défaillance de ce composant dans des conditions de fonctionnement normal.
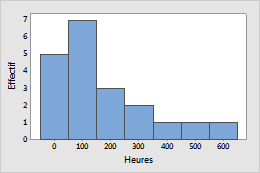
Exemple 2 : Filaments
Une société fabriquant des ampoules produit des filaments à incandescence qui ne devraient pas s'user pendant une période prolongée d'utilisation normale. Elle souhaite garantir leur fonctionnement sur 10 ans. Les ingénieurs soumettent les ampoules à des contraintes afin de simuler une utilisation à long terme et enregistrent le nombre de mois de fonctionnement de chaque ampoule avant défaillance.
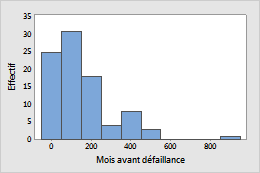
Fonction de densité de probabilité et fonction de risque pour la loi exponentielle
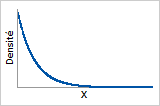
Fonction de densité de probabilité
La fonction de densité de probabilité montre que les données de défaillance sont asymétriques vers la droite.
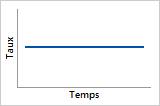
Fonction de risque
La fonction de risque montre que le risque de défaillance est constant.
