Sur ce thème
Récapitulatif des plaintes actuelles relatives à la garantie
Après le reformatage des données à l'aide de la fonction Pré-traiter les données de garantie, les données sont tronquées par intervalle et regroupées dans des intervalles notés au format (t0, t1), (t1, t2),..., (tk-1, tk), tel que chaque intervalle (ti-1, ti) contient ni défaillances (si ti est fini) ou ni suspensions (si ti est infini), i = 1, 2, ..., k.
Nombre total d'unités = nombre total d'unités expédiées jusqu'à présent
Nombre de défaillances observé = nombre d'unités expédiées et ayant connu une défaillance lors de la période de garantie

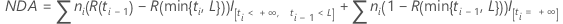
Nombre d'unités à risque pour les périodes futures = nombre total d'unités tronquées à droite sous garantie
Notation
| Terme | Description |
|---|---|
| R(t) | fonction de fiabilité |
Remarque
Pour plus d'informations sur la fonction de fiabilité, reportez-vous à la rubrique Probabilités de survie.
Futures défaillances prévues
Les calculs pour le nombre attendu de futures défaillances reposent uniquement sur les "unités suspendues" (unités tronquées à droite). Les unités ayant déjà rencontré une défaillance n'ont pas de répercussion sur les futures défaillances.
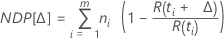
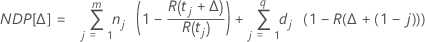
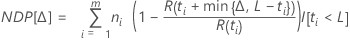
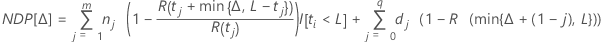
Notation
| Terme | Description |
|---|---|
| ti | temps de suspension |
| ni | nombre d'unités suspendues à l'instant ti, i = 1, 2, ..., m |
| m | nombre de temps de suspension distincts |
| R(t) | fonction de fiabilité. Pour plus d'informations, reportez-vous à la rubrique Probabilités de survie. |
Intervalles de confiance pour le nombre de défaillances attendu
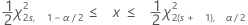
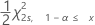
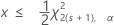
Ces bornes et intervalles de confiance reposent sur l'hypothèse selon laquelle les défaillances se produisent selon un procédé de Poisson approximatif avec un taux constant.
Notation
| Terme | Description |
|---|---|
| s | nombre de défaillances prévu calculé (la statistique) |
| x | nombre de défaillances prévu réel (le paramètre) |
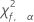 | 100(1-α)e percentile de la loi du Khi deux avec f degrés de liberté |
| α | seuil de signification (alpha) |
Graphiques
- Diagramme du nombre de défaillances prévu
- Le nombre de défaillances prévu est représenté en fonction des périodes futures. L'étendue de valeurs de l'axe des x correspond à la plage des périodes futures. Si vous n'indiquez pas de périodes futures (c'est-à-dire, si la sous-commande PREDICT n'est pas définie), l'étendue de valeurs de l'axe des x est (0, 5].
- Diagramme du coût des défaillances prévu
- Si vous indiquez un coût moyen par défaillance (c'est-à-dire, si vous utilisez la sous-commande COST), le coût prévu des défaillances est représenté en fonction aux périodes futures. L'étendue de valeurs de l'axe des x correspond à la plage des périodes futures. Si vous n'indiquez pas de périodes futures (c'est-à-dire, si la sous-commande PREDICT n'est pas définie), l'étendue de valeurs de l'axe des x est (0, 5].
