Sur ce thème
- Estimation ponctuelle d’un centile pour un pourcentage donné
- Erreur type d’un centile pour un pourcentage donné
- Intervalle de confiance repère d’un centile pour un pourcentage donné
- Intervalle de confiance repère de la probabilité de défaillance ou de la probabilité de survie à une valeur de contrainte donnée
- Références
Estimation ponctuelle d’un centile pour un pourcentage donné
Le pe centile, xp, est le niveau de stress nécessaire pour une réponse p.
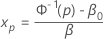
Pour trouver l’estimation de xp, utilisez la formule suivante :
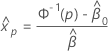
où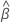 
et 
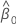sont les estimations du maximum de vraisemblance 
et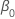 
.
Les distributions log-emplacement pour l’analyse Probit sont les distributions lognormale, loglogistique et Weibull. Pour les distributions log-emplacement, les formules précédentes estiment le percentile sur l’échelle logarithmique. Pour estimer le percentile sur l’échelle des données avec ces distributions, utilisez la formule suivante.
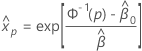
Erreur type d’un centile pour un pourcentage donné
Le calcul de l’erreur type d’un percentile utilise la méthode delta. L’erreur-type du centile estimé est calculée selon la formule suivante.
lorsque l’écart de 
se présente sous la forme suivante :
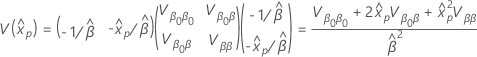
et la matrice variance-covariance de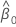 
et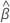 
se présente sous la forme suivante :
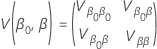
Les distributions log-emplacement pour l’analyse Probit sont les distributions lognormale, loglogistique et Weibull. Pour les distributions log-emplacement, les formules précédentes estiment la variance de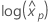 
. Définitions de la variance et de la matrice variance-covariance en termes de 
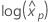suivre.
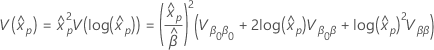
Intervalle de confiance repère d’un centile pour un pourcentage donné
Les deux faces, 100(1 - 
) pour 
est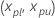 
avec les équations suivantes.
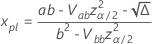
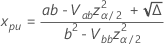
où
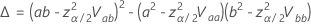
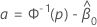
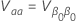
Les distributions log-emplacement pour l’analyse Probit sont les distributions lognormale, loglogistique et Weibull. Pour les distributions log-emplacement, les formules précédentes estiment l’intervalle sur l’échelle logarithmique. Pour estimer l’intervalle à l’échelle des données, exponentiez les limites de confiance dans les formules précédentes.
Intervalle de confiance repère de la probabilité de défaillance ou de la probabilité de survie à une valeur de contrainte donnée
Les deux faces, 100(1 - 
) pour la probabilité de défaillance,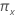 
est 
. Pour la probabilité de survie, 
, l’intervalle est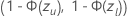 
. Les formules suivantes donnent les calculs.
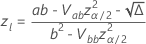
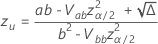
où
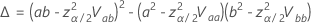
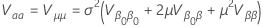
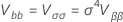
et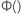 
est la fonction de distribution cumulative de la distribution pour l’analyse.
Les distributions log-emplacement pour l’analyse Probit sont les distributions lognormale, loglogistique et Weibull. Pour les distributions log-location, remplacez la définition suivante.
Références
La dérivation des intervalles de confiance repère utilise le théorème de Fieller. Le théorème de Fieller se trouve dans la référence suivante.
Finney, D. J. (1971). Probit analysis, (Third edition), London: Cambridge University Press.
Pour plus d’informations sur le modèle probit et l’estimation des percentiles, consultez la référence suivante.
Cox, D. R. and Snell, E. J. (1989). The analysis of binary data (Second edition), London: Chapman & Hall.
