Méthodes et formules pour les méthodes d'estimation pour la fonction Analyse de répartition non paramétrique (troncature à droite)

L'estimateur de Kaplan-Meier, également appelé estimateur produit-limite, peut être utilisé pour calculer les probabilités de survie dans les ensembles de données non paramétriques comportant plusieurs défaillances et suspensions. L'équation de l'estimateur est la suivante :

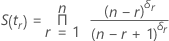
Avec S(t₀) = 1 et t₀ = 0.

Fonction de risque empirique

La fonction de risque décrit le taux de défaillance associé à un intervalle. La fonction de risque est de 0 avant la première observation tronquée. La fonction de risque change uniquement au niveau des observations non tronquées. Minitab ne représente pas la fonction de risque après le dernier point de données non tronqué.

En cas de valeurs ex aequo, Minitab utilise celle qui a le rang le plus élevé pour estimer la fonction de risque. Reportez-vous à Nelson¹ pour plus de détails.

Durée moyenne avant défaillance

Pour les données non tronquées, la durée moyenne avant défaillance est identique au temps de défaillance moyen. La formule générale à utiliser avec les données tronquées ou non tronquées est la suivante :

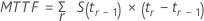
Par ailleurs, lorsque la plus grande observation est tronquée, Minitab utilise le temps de la plus grande observation non tronquée comme limite de temps pour le calcul. Reportez-vous à Lee² pour plus de détails.

Erreur type de la MTTF

L'erreur type de la durée moyenne avant défaillance est égale à la racine carrée de la variance. Lorsque aucune observation n'est tronquée, Minitab calcule une estimation non biaisée comme suit :

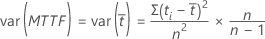
Si des données sont tronquées, l'estimation non biaisée de la variance est obtenue à l'aide de la formule suivante :

Etant donné la forme de la fonction de risque empirique, les zones situées sous la courbe de survie, A_r, sont des rectangles, dont la hauteur est égale à la fonction de survie et la longueur est égale aux intervalles entre les observations non tronquées.

Notation

Terme	Description
tr	temps du point de données ayant le rang r
r	rang du point de données, où la défaillance la plus ancienne a le rang le plus bas
n	nombre total d'unités
δr	0 si la je observation est tronquée ou 1 si la je observation n'est pas tronquée
c	nombre de points de données jusqu'à la prochaine observation non tronquée
S(tr)	fonction de survie empirique au temps tr
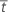	contrainte moyenne associée à la défaillance
Ar	aire sous la courbe du diagramme de survie à droite de tr
m	nombre total d'observations non tronquées

Références

1. W. Nelson (1982), Applied Life Data Analysis, John Wiley & Sons, Inc. 133.

2. Elisa T. Lee (1992), Statistical Methods for Survival Data Analysis, deuxième édition, John Wiley & Sons, Inc. 73-76.

Le modèle actuariel est une analyse non paramétrique alternative qui affiche les informations concernant les regroupements de temps de défaillance. La méthode de Kaplan-Meier suppose que les suspensions effectuées dans un intervalle se produisent à la fin de ce dernier, après la survenue des défaillances. Le modèle actuariel de Minitab suppose que les suspensions surviennent au centre de l'intervalle, ce qui réduit le nombre d'unités disponibles dans l'intervalle. L'estimation de la fonction de survie à l'aide de la méthode actuarielle est calculée comme suit :

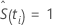pour i = 0

pour i > 0

Fonction de risque empirique

La fonction de risque décrit le taux de défaillance associé à un intervalle. Avec l'estimation actuarielle, vous supposez que le calcul concerne le point central de l'intervalle. Sur le diagramme de risque, la fonction est tracée de point central en point central. Pour plus d'informations, reportez-vous aux références fournie après la section Notation.

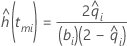
Notation

Terme	Description
ni	nombre d'unités entrant dans un intervalle
di	nombre de défaillances dans l'intervalle
n'i
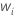	nombre d'éléments tronqués dans un intervalle
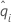	Probabilité conditionnelle d'un événement, qui est égale à di/n'i
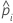tmi	temps au point central de l'intervalle actuariel
bi	longueur de l'intervalle actuariel

Références

Collett, D. (1994), Modelling Survival Data in Medical Research, Chapman and Hall.

Lee, Elisa T. (1992), Statistical Methods for Survival Data Analysis, deuxième édition, John Wiley & Sons.

Turnbull^{1, 2} a développé un algorithme itératif pour calculer l'estimation non paramétrique de la fonction de répartition cumulative des données par le maximum de vraisemblance. Cette méthode s'applique à des situations plus générales, par exemple, lorsque les intervalles se chevauchent.

Minitab affiche des résultats résumant l'estimation de Turnbull des probabilités correspondant aux intervalles, ainsi que les erreurs types associées à ces probabilités.

Références

Indépendamment de la méthode d'estimation, Minitab utilise une approximation par la loi normale pour calculer les intervalles de confiance. Les intervalles de confiance sont déterminés comme suit :

Formule

Estimation de la probabilité de survie z_α × Erreur type de l'estimation

Notation

Terme	Description
zα	valeur critique supérieure 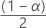pour la loi normale standard
α	niveau de confiance