Sur ce thème
Estimations des paramètres
Formule
| Loi de distribution | Paramètres |
|---|---|
|
Plus petite valeur extrême Normale Logistique |
μ = emplacement, σ = échelle, σ > 0 |
|
Log-normale Log-logistique |
μ = emplacement, μ > 0 σ = échelle, σ > 0 |
|
Log-normale à trois paramètres Log-logistique à 3 paramètres |
μ = emplacement, μ > 0 σ = échelle, σ > 0 λ = seuil. |
|
Weibull |
α = échelle, α = exp(μ) β = forme, β = 1/σ |
|
Weibull à 3 paramètres |
α = échelle, α = exp(μ) β = forme, β = 1/σ λ = seuil, |
|
Exponentielle |
θ = échelle, θ > 0 |
|
Exponentielle à 2 paramètres |
θ = échelle, θ > 0 λ = seuil, |
Erreur type des estimations de paramètres
L'erreur type est l'écart type de l'estimation du paramètre. L'erreur type fournit une mesure de la variabilité de chaque estimation.
 ,
,  ,
,  ,
,  ,
,  , et
, et  désignent l'erreur type de l'EMaxV de μ, σ, α, β, θ et λ. Chaque erreur type est calculée comme la racine carrée de l'élément diagonal correspondant de l'inverse de la matrice des informations de Fisher.
désignent l'erreur type de l'EMaxV de μ, σ, α, β, θ et λ. Chaque erreur type est calculée comme la racine carrée de l'élément diagonal correspondant de l'inverse de la matrice des informations de Fisher.
Limites de confiance pour les estimations des paramètres
Formule
| Loi de distribution | Paramètre | Limite de confiance inférieure | Limite de confiance supérieure |
|---|---|---|---|
| Plus petites valeurs extrêmes, normale, logistique log-normale et log-logistique | Emplacement, μ |
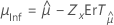 |
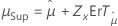 |
| Echelle , σ |
 |
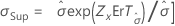 |
|
| Log-normale à 3 paramètres, log-logistique à 3 paramètres | Emplacement, μ |
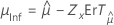 |
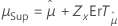 |
| Echelle , σ |
 |
 |
|
| Seuil, λ |
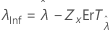 |
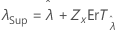 |
|
| Weibull | Forme, β |
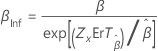 |
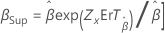 |
| Echelle, α |
 |
 |
|
|
Weibull à 3 paramètres |
Forme, β |
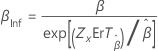 |
 |
|
Echelle, α |
 |
 |
|
|
Seuil, λ |
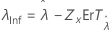 |
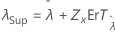 |
|
| Exponentielle | Echelle |
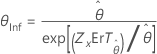 |
 |
| Exponentielle à 2 paramètres | Echelle, θ |
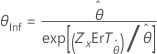 |
 |
| Seuil, λ |
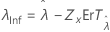 |
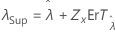 |
Remarque
Pour certaines données, la fonction de vraisemblance est illimitée et fournit donc des estimations incohérentes pour les lois ayant un paramètre de seuil (comme la loi exponentielle à 2 paramètres). Lorsque cela se produit, la matrice de variance-covariance des paramètres estimés ne peut pas être déterminée de manière numérique. Dans ce cas, Minitab suppose que 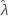 est fixe, ce qui implique que ErT (
est fixe, ce qui implique que ErT (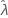 ) = 0. Les bornes supérieure et inférieure pour
) = 0. Les bornes supérieure et inférieure pour 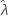 sont
sont 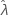 .
.
Notation
| Terme | Description |
|---|---|
| zx | valeur critique supérieure 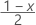 pour la loi normale standard, où 100x % est le niveau de confiance et 0 < x < 1. pour la loi normale standard, où 100x % est le niveau de confiance et 0 < x < 1. |




