Fiabilité fournie
Si vous définissez l'objectif de fiabilité par une durée et une valeur de fiabilité, Minitab calcule d'abord le paramètre recherché à l'aide de la formule indiquée dans le tableau suivant pour la loi spécifiée.
Minitab calcule ensuite le temps de test ou l'effectif d'échantillon nécessaires de la même manière que dans le cas d'un test de corroboration.
| Loi (paramètre) | Paramètre à démontrer |
|---|---|
| Weibull (échelle) |
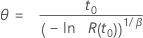 |
| Exponentielle (moyenne) |
 |
|
Plus petites valeurs extrêmes (emplacement) Normale (moyenne) Logistique (moyenne) |
 |
|
Log-normale (log-emplacement) Log-logistique (log-emplacement) |
 |
Notation
| Terme | Description |
|---|---|
| t | durée |
| R(t) | fonction de fiabilité |
| θ | échelle (Weibull) ou moyenne (exponentielle) |
| β | paramètre de forme (Weibull) |
| σ | paramètre d'échelle (log-normale, log-logistique, logistique, normale, plus petites valeurs extrêmes) |
| μ | moyenne (normale, logistique) ou log-emplacement (log-normale, log-logistique) |
| Φ-1 | fonction CDF inverse de la loi correspondante |
P-ième percentile fourni
Si vous définissez l'objectif de fiabilité en fonction du Pe percentile (tp), Minitab calcule d'abord le paramètre recherché à l'aide de la formule indiquée dans le tableau suivant pour la loi spécifiée.
Minitab calcule ensuite le temps de test ou l'effectif d'échantillon nécessaires de la même manière que dans le cas d'un test de corroboration.
| Loi (paramètre) | Paramètre à démontrer |
|---|---|
| Weibull (échelle) |
 |
| Exponentielle (moyenne) |
 |
|
Plus petites valeurs extrêmes (emplacement) Normale (moyenne) Logistique (moyenne) |
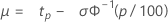 |
|
Log-normale (log-emplacement) Log-logistique (log-emplacement) |
 |
Notation
| Terme | Description |
|---|---|
| t | durée |
| R(t) | fonction de fiabilité |
| p | percentile |
| α | échelle (Weibull) |
| θ | moyenne (exponentielle) |
| μ | moyenne (normale, logistique), emplacement (plus petites valeurs extrêmes) ou log-emplacement (log-normale, log-logistique) |
| Φ-1 | fonction CDF inverse de la loi correspondante |
MTTF fournie
Si vous définissez l'objectif de fiabilité en fonction de la durée moyenne avant défaillance (MTTF), Minitab calcule d'abord le paramètre recherché à l'aide de la formule indiquée dans le tableau suivant pour la loi spécifiée.
Minitab calcule ensuite le temps de test ou l'effectif d'échantillon nécessaires de la même manière que dans le cas d'un test de corroboration.
| Loi (paramètre) | Paramètre à démontrer |
|---|---|
| Weibull (échelle) |
 |
| Exponentielle (moyenne) |
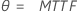 |
|
Normale (moyenne) Logistique (moyenne) |
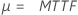 |
|
Log-normale (log-emplacement) |
 |
|
Log-logistique (log-emplacement) |
 |
|
Plus petites valeurs extrêmes (emplacement) |
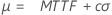 |
Notation
| Terme | Description |
|---|---|
| α | échelle (Weibull) |
| σ | échelle (log-normale, log-logistique, plus petites valeurs extrêmes) |
| β | forme (Weibull) |
| θ | moyenne (exponentielle) |
| μ | moyenne (normale, logistique), emplacement (plus petites valeurs extrêmes) ou log-emplacement (log-normale, log-logistique) |
| Durée moyenne avant défaillance (MTTF) | durée moyenne avant défaillance |
| c | constante d'Euler ≈ 0.5772 |
| Γ | fonction gamma |
