Fonctions de fiabilité et de fiabilité inverse
Plus petites valeurs extrêmes
- Fiabilité
-
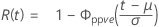
- Fiabilité inverse
-

où
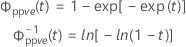
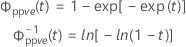
| Terme | Description |
|---|---|
| t | durée |
| μ | paramètre d'emplacement |
| σ | paramètre d'échelle |
| Φppve(t) | CDF de la loi des plus petites valeurs extrêmes |
| Φ-1ppve(t) | CDF inverse de la loi des plus petites valeurs extrêmes |
Weibull
- Fiabilité
-
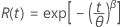
- Fiabilité inverse
-

| Terme | Description |
|---|---|
| t | durée |
| p | probabilité |
| β | paramètre de forme |
| θ | paramètre d'échelle |
Exponentielle
- Fiabilité
-

- Fiabilité inverse
-
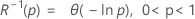
| Terme | Description |
|---|---|
| t | durée |
| p | probabilité |
| θ | paramètre de moyenne |
Normale
- Fiabilité
-
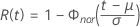
- Fiabilité inverse
-

| Terme | Description |
|---|---|
| t | durée |
| μ | paramètre d'emplacement |
| σ | paramètre d'échelle |
| Φni(t) | CDF de la loi normale |
| Φ-1ni(t) | CDF inverse de la loi normale |
Log-normale
- Fiabilité
-

- Fiabilité inverse
-

| Terme | Description |
|---|---|
| t | durée |
| μ | paramètre d'emplacement |
| σ | paramètre d'échelle |
| Φni(t) | CDF de la loi normale |
| Φ-1ni(t) | CDF inverse de la loi normale |
Logistique
- Fiabilité
-
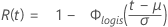
- Fiabilité inverse
-
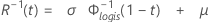
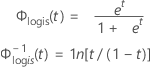
| Terme | Description |
|---|---|
| t | durée |
| μ | paramètre d'emplacement |
| σ | paramètre d'échelle |
| Φlogis(t) | CDF de la loi logistique |
| Φ-1logis(t) | CDF inverse de la loi logistique |
Log-logistique
- Fiabilité
-

- Fiabilité inverse
-
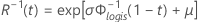
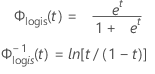
| Terme | Description |
|---|---|
| t | durée |
| μ | paramètre d'emplacement |
| σ | paramètre d'échelle |
| Φlogis(t) | CDF de la loi logistique |
| Φ-1logis(t) | CDF inverse de la loi logistique |
Equation
L'équation pour un plan de test à m défaillances est la suivante :

Notation
| Terme | Description |
|---|---|
| α | alpha (égal à 1 – le niveau de confiance) |
| R | fonction de fiabilité ou de survie au temps t |
| N | nombre minimal d'unités à tester |
