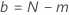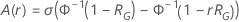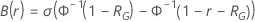Les calculs de la probabilité de réussite d'un plan de test dépendent de la loi qui modélise les défaillances. Pour une loi log-emplacement-échelle, la probabilité est une fonction du rapport d'amélioration. Pour une loi emplacement-échelle, la probabilité est une fonction du degré d'amélioration. L'expression des formules se divise parfaitement en deux cas, selon si vous spécifiez l'effectif d'échantillon ou le temps de test.
Effectif d'échantillon
 satisfait à l'équation suivante :
satisfait à l'équation suivante :
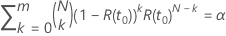
 , la solution,
, la solution,  , de l'équation se calcule selon la formule suivante :
, de l'équation se calcule selon la formule suivante :
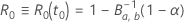
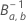 est la fonction de répartition inverse de la loi bêta avec les paramètres de forme suivants :
est la fonction de répartition inverse de la loi bêta avec les paramètres de forme suivants :
 , inversez la fonction
, inversez la fonction  . L'inversion dépend de la famille de la loi.
. L'inversion dépend de la famille de la loi.
- Famille log-emplacement-échelle

- Famille emplacement-échelle
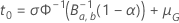
 et de l'amélioration :
et de l'amélioration :
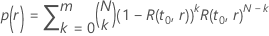
où 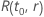 est la fonction de fiabilité du modèle de loi par rapport à
est la fonction de fiabilité du modèle de loi par rapport à  et
et 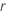 .
.
- Famille log-emplacement-échelle

- Famille emplacement-échelle
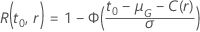
Le tableau suivant donne la fonction de  pour la famille de la loi et l'objectif du test :
pour la famille de la loi et l'objectif du test :
| Objectif de fiabilité | ||||
|---|---|---|---|---|
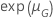 |
 |
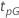 |
 |
|
| Log-emplacement-échelle |
 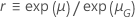 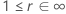 |
 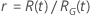  |
 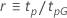 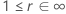 |
  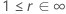 |
| Objectif de fiabilité | ||||
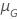 |
 |
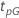 |
 |
|
| Emplacement-échelle |
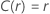  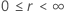 |
 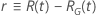  |
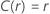  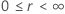 |
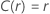  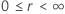 |
Exemple de 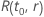 pour la loi de Weibull
pour la loi de Weibull
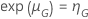 et un effectif d'échantillon donné, la probabilité de réussite se calcule selon la formule suivante :
et un effectif d'échantillon donné, la probabilité de réussite se calcule selon la formule suivante :
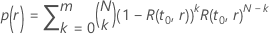
où

Temps de test
 satisfait à l'équation suivante :
satisfait à l'équation suivante :

 ), la solution de l'équation,
), la solution de l'équation, 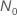 , se calcule selon la formule suivante :
, se calcule selon la formule suivante :

 ), il n'existe pas de solution de forme fermée. Meeker et Escobar (1998)1 donnent la solution approximative suivante :
), il n'existe pas de solution de forme fermée. Meeker et Escobar (1998)1 donnent la solution approximative suivante :
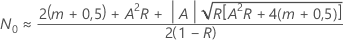
où

Minitab trouve la solution exacte numériquement lorsque  .
.
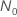 et de l'amélioration :
et de l'amélioration :
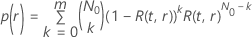
où 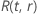 est la fonction de fiabilité du modèle de loi par rapport à
est la fonction de fiabilité du modèle de loi par rapport à  et
et 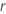 .
.
- Famille log-emplacement-échelle

- Famille emplacement-échelle
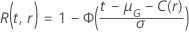
La fonction  présente les mêmes définitions que lorsque les spécifications du test incluent l'effectif d'échantillon.
présente les mêmes définitions que lorsque les spécifications du test incluent l'effectif d'échantillon.
Exemple de 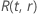 pour la loi de Weibull
pour la loi de Weibull
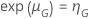 et un temps de test donné, la probabilité de réussite se calcule selon la formule suivante :
et un temps de test donné, la probabilité de réussite se calcule selon la formule suivante :
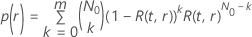
où

Notation
| Terme | Description |
|---|---|
| N | effectif d'échantillon pour le plan lorsque les spécifications du test incluent l'effectif d'échantillon |
| m | nombre d'unités qui présentent une défaillance au cours du test |
 | seuil de signification, de sorte que le niveau de confiance pour le test de démonstration est  |
 | paramètre d'échelle |
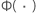 | fonction de répartition de la loi standard pour la loi sélectionnée log-emplacement-échelle ou emplacement-échelle |
 | fonction de répartition inverse de la loi standard pour la loi sélectionnée log-emplacement-échelle ou emplacement-échelle |
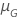 | paramètre d'emplacement pour la loi qui répond à l'objectif du test |
 | paramètre de forme de la loi Weibull |
 | temps de test lorsque les spécifications du test incluent l'effectif d'échantillon |
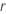 | rapport d'amélioration des lois log-emplacement-échelle ou degré d'amélioration des lois emplacement-échelle |
 | fiabilité à l'instant t visée pour le test |
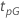 | percentile au pourcentage p visé pour le test |
 | durée moyenne avant défaillance visée pour le test |
 | temps de test lorsque les spécifications du test incluent le temps de test |
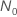 | effectif d'échantillon lorsque les spécifications du test incluent le temps de test |