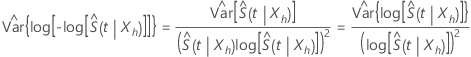Sur ce thème
Fonction de survie
La fonction de survie utilise les définitions suivantes :
| Terme | Description |
|---|---|
 | les heures distinctes et ordonnées de l’événement |
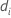 | le nombre d'événements à la fois  |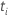
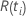 | le risque fixé à ce moment-là 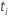 , qui est l’ensemble de toutes les unités d’échantillonnage qui n’ont pas encore échoué avant l’heure  |
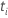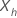 | le vecteur p-component des valeurs de covariable qui représente un point de données nouveau ou existant |
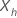, la fonction de survie du modèle des risques proportionnels de Cox se présente sous la forme suivante :
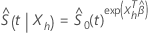
où
et
La fonction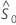 
estime la fonction de survie d’un individu lorsque les valeurs de toutes les covariables sont 0. La fonction 
est l’estimateur de Breslow du taux de danger cumulatif de référence. La fonction 
est une fonction de pas qui saute aux heures d’événement observées.
Intervalles de confiance
Dans des conditions de régularité douce, l’estimateur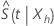 
a une loi normale asymptotique avec une moyenne 
et variance asymptotique sous la forme suivante :
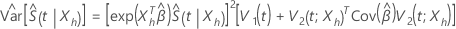
où
et
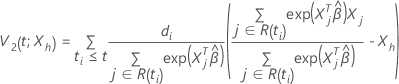
Un intervalle de confiance direct de la méthode wald est disponible mais est moins précis car la distribution de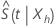 
est gravement biaisé. De plus, les limites de confiance de ces intervalles sont souvent en dehors de l’intervalle [0, 1]. La distribution du logarithme de 
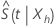est moins biaisé et converge plus rapidement vers la distribution normale. Minitab utilise les transformations suivantes pour calculer les intervalles de confiance.
Transformation logarithmique
Minitab calcule un intervalle de confiance pour 
et rétro-transforme les limites de confiance pour fournir l’intervalle de confiance pour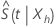 
. En utilisant cette approche, un intervalle de confiance approximatif de 100 (1 – α) pour 
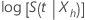, se calcule selon la formule suivante :
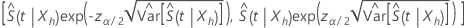
où 
estime la variance asymptotique de 
, se calcule selon la formule suivante :
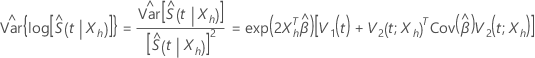
Placer la limite de confiance supérieure pour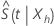 
dépasse 1, puis Minitab utilise 1 comme limite supérieure.
Transformation par logarithme népérien
La transformation log-log garantit que l’intervalle de confiance pour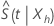 
est dans l'intervalle (0, 1). Minitab calcule un intervalle de confiance pour l
et rétro-transforme les limites de confiance pour fournir l’intervalle de confiance pour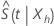 
. En utilisant cette méthode, un intervalle de confiance approximatif de 100 (1 – α) pour 
, se calcule selon la formule suivante :
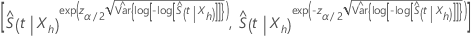
où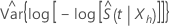 
estime la variance asymptotique de 
, se calcule selon la formule suivante :
