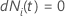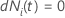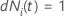| Terme | Description |
|---|---|
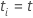
 | les heures distinctes et ordonnées de l’événement |
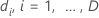 | le
nombre d'événements au temps 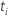 |
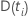 | l’ensemble de toutes les unités qui vivent l’événement à un moment donné
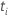 |
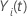 | une variable indicatrice qui a la valeur 1 si le sujet
i est à risque au temps
t et 0 sinon, ce qui équivaut à 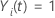 si si
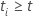 et et
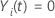 sinon
sinon |
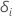 | un indicateur indiquant si le sujet
i est censuré, tel que 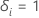 si le sujet
i a vécu l’événement et si le sujet
i a vécu l’événement et 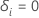 sinon
sinon |
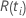 | le risque fixé à ce moment-là 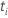 ,
qui est l’ensemble de toutes les unités d’échantillonnage qui n’ont pas encore
échoué avant l’heure ,
qui est l’ensemble de toutes les unités d’échantillonnage qui n’ont pas encore
échoué avant l’heure 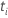 |
 | le nombre d’événements pour le sujet i jusqu’à l’heure t incluse |
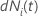 | le changement de  pour le sujet
i à l’instant
t tel que
pour le sujet
i à l’instant
t tel que
|
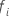 | le premier moment de l’événement auquel le sujet i est dans l’ensemble de risques |
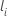 | l’heure du dernier événement à laquelle le sujet i est dans l’ensemble de risques |
Valeurs résiduelles de Cox-Snell
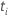 ,
se calcule selon la formule suivante :
,
se calcule selon la formule suivante : 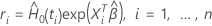
où  est l’estimateur de Breslow du taux de danger cumulatif de référence :
est l’estimateur de Breslow du taux de danger cumulatif de référence :

 est une fonction de pas avec des sauts aux heures d’événement observées. Valeur
du modèle à l'instant 0.
est une fonction de pas avec des sauts aux heures d’événement observées. Valeur
du modèle à l'instant 0.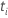 ,
se calcule selon la formule suivante :
,
se calcule selon la formule suivante : 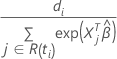

Pour l’approximation d’Efron, le résidu de Cox-Snell a la forme suivante :
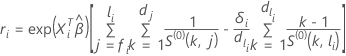
où 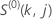 ,
se calcule selon la formule suivante :
,
se calcule selon la formule suivante :
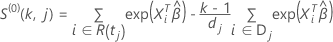
Pour 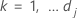
où 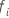 est le premier événement auquel le sujet
i est dans l’ensemble de risques et
est le premier événement auquel le sujet
i est dans l’ensemble de risques et 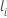 est le dernier moment de l’événement auquel le sujet
i est dans l’ensemble de risques.
est le dernier moment de l’événement auquel le sujet
i est dans l’ensemble de risques.
Résidus de martingale
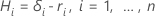
où 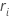 est le résidu de Cox-Snell et dépend de la méthode de manutention des attaches.
Additif,
est le résidu de Cox-Snell et dépend de la méthode de manutention des attaches.
Additif, 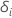 est un indicateur pour savoir si le sujet
i est censuré, tel que
est un indicateur pour savoir si le sujet
i est censuré, tel que 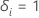 si le sujet
i a vécu l’événement et
si le sujet
i a vécu l’événement et 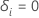 sinon
sinon
Valeurs résiduelles de la somme des carrés d'écart

où 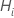 est le résidu de Martingale pour le sujet
i.
est le résidu de Martingale pour le sujet
i.
Vecteur résiduel de Schoenfeld
Le vecteur résiduel de Schoenfeld est un vecteur p-composante. Pour le sujet i avec le temps d’événement t, le vecteur résiduel de Schoenfeld a la forme suivante :
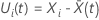
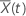 est la moyenne pondérée des covariables par rapport au risque fixé à l’instant
t. La moyenne pondérée se présente sous la forme suivante :
est la moyenne pondérée des covariables par rapport au risque fixé à l’instant
t. La moyenne pondérée se présente sous la forme suivante : 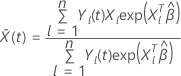
où 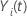 est une variable indicatrice qui a la valeur 1 si le sujet
i est à risque au temps
t et 0 sinon, ce qui équivaut à
est une variable indicatrice qui a la valeur 1 si le sujet
i est à risque au temps
t et 0 sinon, ce qui équivaut à 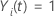 si
si
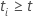 et
et
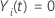 sinon
sinon
Si le sujet ne rencontre pas l’événement au temps t, le vecteur contient des valeurs manquantes.
Le calcul du vecteur résiduel de Schoenfeld dépend de la méthode de manutention des attaches. Pour l’approximation de Breslow, le vecteur résiduel de Schoenfeld a la forme suivante :
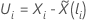
où
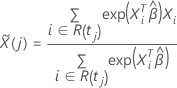
Pour l’approximation d’Efron, le vecteur résiduel de Schoenfeld a la forme suivante :
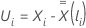
où
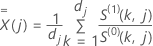
La fonction 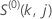 a
la même définition que pour le résidu de Cox-Snell :
a
la même définition que pour le résidu de Cox-Snell :
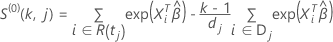
et
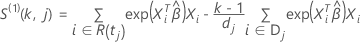
Pour 
Vecteur résiduel de Schoenfeld à l’échelle
Le vecteur résiduel de Schoenfeld à l’échelle a la forme suivante :

où  est le
nombre observé de temps de survie non censurés et
est le
nombre observé de temps de survie non censurés et 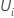 est le vecteur résiduel de Schoenfeld.
est le vecteur résiduel de Schoenfeld.
Vecteur résiduel de score
Le calcul du vecteur résiduel de score dépend de la méthode d’approximation des égalités dans les temps d’événement. Pour l’approximation de Breslow, le vecteur résiduel score a la forme suivante :
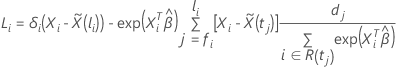
où
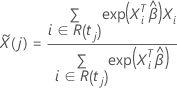
Pour l’approximation d’Efron, le vecteur résiduel de score a la forme suivante :
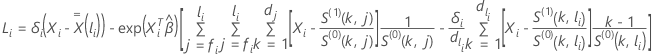
où 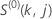 ,
,
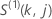 et
et  ont les mêmes définitions que pour le vecteur résiduel de Schoenfeld :
ont les mêmes définitions que pour le vecteur résiduel de Schoenfeld :
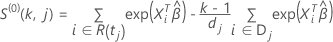
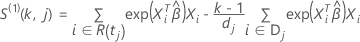
et
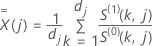
Pour 
DFBeta
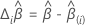

où 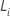 est le vecteur résiduel de score. Pour plus de détails sur les seuil,
reportez-vous à
est le vecteur résiduel de score. Pour plus de détails sur les seuil,
reportez-vous à  ,
aller à
Méthodes et formules pour les coefficients et équation de régression pour Ajuster le modèle de Cox avec des prédicteurs fixes uniquement.
,
aller à
Méthodes et formules pour les coefficients et équation de régression pour Ajuster le modèle de Cox avec des prédicteurs fixes uniquement.