Méthodes et formules pour les modèles de test accéléré de durée de vie pour la fonction Plan de test accéléré de durée de vie

Linéaire

Terme	Description
Y_p	moment de défaillance ou log du moment de défaillance
β₀	ordonnée à l'origine (constante)
β₁	coefficient de régression
σ	réciproque du paramètre de forme (loi de Weibull) ou du paramètre d'échelle (autres lois)
Φ^-1(p)	p-ième quantile de la loi de distribution des durées de vie normalisée

où la valeur en numérateur (11604,53) est la valeur inversée de la constante de Boltzman et la valeur en dénominateur (273,16) est le zéro absolu.

Terme	Description
Y_p	moment de défaillance ou log du moment de défaillance
β₀	ordonnée à l'origine (constante)
β₁	coefficient de régression
σ	réciproque du paramètre de forme (loi de Weibull) ou du paramètre d'échelle (autres lois)
Φ^-1(p)	p-ième quantile de la loi de distribution des durées de vie normalisée

Terme	Description
Y_p	moment de défaillance ou log du moment de défaillance
β₀	ordonnée à l'origine (constante)
β₁	coefficient de régression
σ	réciproque du paramètre de forme (loi de Weibull) ou du paramètre d'échelle (autres lois)
Φ^-1(p)	p-ième quantile de la loi de distribution des durées de vie normalisée

Terme	Description
Y_p	moment de défaillance ou log du moment de défaillance
β₀	ordonnée à l'origine (constante)
β₁	coefficient de régression
σ	réciproque du paramètre de forme (loi de Weibull) ou du paramètre d'échelle (autres lois)
Φ^-1(p)	p-ième quantile de la loi de distribution des durées de vie normalisée

L'accélération normalisée est calculée comme suit :

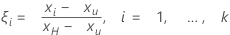
Le modèle de test accéléré de durée de vie normalisé est le suivant :

Terme	Description
k	nombre de niveaux de la variable d'accélération (sans inclure le niveau d'utilisation normale)
X_i	niveau de la variable d'accélération
X_U	Niveau d'utilisation
X_H	niveau le plus élevé de la variable d'accélération