Deux problèmes peuvent empêcher la convergence des estimations du maximum de vraisemblance pour les coefficients : la séparation complète et la séparation quasi-complète.
Séparation complète
On parle de séparation complète lorsqu'une combinaison linéaire de prédicteurs génère une prévision parfaite de la variable de réponse. Par exemple, dans l'ensemble de données suivantes, si X ≤ 4 alors Y = 0. Si X > 4 alors Y = 1.
| Y | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |
Séparation quasi-complète
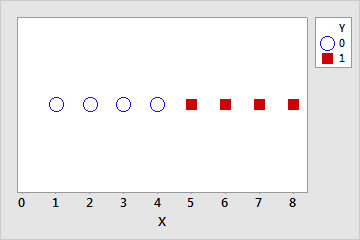
La séparation quasi-complète est semblable à la séparation complète. Les prédicteurs génèrent une prévision parfaite de la variable de réponse pour la plupart des valeurs des prédicteurs, mais pas pour toutes. Par exemple, dans l'ensemble de données précédent, pour l'une des valeurs où X = 4, laissez Y = 1 à la place de 0. Désormais, si X < 4 alors Y = 0, si X > 4 alors Y = 1, mais si X = 4 alors Y pourrait être 0 ou 1. Ce chevauchement au milieu des données rend la séparation quasi-complète.
| Y | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |

Causes et solutions
Souvent, une séparation apparaît lorsque la quantité de données n'est pas suffisante pour observer des événements à faibles probabilités. Plus le nombre de prédicteurs dans le modèle est élevé, plus la séparation est probable car les effectifs d'échantillons des groupes individuels dans les données sont plus faibles.
Bien que Minitab affiche un avertissement lorsqu'il détecte une séparation, plus le nombre de prédicteurs dans le modèle est élevé, plus il est difficile d'identifier la cause de la séparation. L'inclusion de termes d'interaction dans le modèle augmente encore la difficulté.
- Augmentez la quantité de données. La séparation survient souvent lorsqu'une catégorie ou une étendue de valeurs d'un prédicteur ne génère qu'une seule valeur de réponse. Un effectif de l'échantillon plus élevé permet d'augmenter la probabilité d'obtenir des valeurs différentes pour la réponse.
- Réfléchissez aux implications de la séparation. Une séparation complète ou quasi-complète peut certes indiquer que l'effectif d'échantillon est trop faible, mais elle peut aussi signaler des relations importantes. Si la véritable probabilité d'un événement pour un niveau ou une combinaison de niveaux donnés est proche de 0 ou 1, ces informations sont importantes.
- Envisagez d'utiliser un autre modèle. Plus le modèle contient de termes, plus la probabilité d'une séparation pour au moins une variable est forte. Lorsque vous sélectionnez les termes du modèle, vous pouvez vérifier si l'exclusion d'un terme permet la convergence des estimations de maximum de vraisemblance. Si un modèle pertinent et n'utilisant pas le terme existe, vous pouvez poursuivre l'analyse avec ce nouveau modèle.
- Vérifiez s'il est possible de combiner des catégories au sein de variables problématiques. Si la combinaison de certaines catégories s'avère raisonnable, la séparation peut disparaître des données. Par exemple, supposons que "Fruit" est une variable du modèle. "Pamplemousses" ne comporte aucun événement en raison du faible nombre d'essais. La combinaison de "Pamplemousses" et de "Oranges" dans la catégorie "Agrumes" élimine la séparation.
Tableau 1. Données avec séparation complète Fruit Evénements Essais Pamplemousses 0 10 Oranges 5 100 Pommes 25 100 Bananes 40 100 Tableau 2. Données avec chevauchement Fruit Evénements Essais Agrumes 5 110 Pommes 25 100 Bananes 40 100 - Vérifiez si une variable de catégorie problématique est une variable regroupée. Si la relation de la variable regroupée avec la réponse ne présente pas de séparation complète, le remplacement des données numériques peut éliminer la séparation. Par exemple, supposons que "Durée d'embauche" est une variable regroupée dans le modèle. Lorsque les données sont exprimées par incréments de 30 jours, le niveau le plus faible ne comporte que des événements et le niveau le plus élevé n'en a aucun, ce qui crée une séparation complète. Le remplacement du nombre de jours dans le modèle élimine la séparation.
Tableau 3. Données avec séparation complète Catégories de durée Evénements Essais 1–90 2 2 91–180 1 2 181–270 1 2 271–360 0 2 Durée exacte Evénements Essais 45 1 1 60 1 1 95 1 1 176 0 1 185 0 1 241 1 1 280 0 1 299 0 1
Lectures complémentaires
Pour plus d'informations sur la séparation, consultez l'ouvrage suivant : Albert et J. A. Anderson (1984), "On the existence of maximum likelihood estimates in logistic regression models" Biometrika 71, 1, 1-10.
