Qu'est-ce qu'une analyse de régression ?
Une analyse de régression génère une équation pour décrire la relation statistique entre un ou plusieurs prédicteurs et la variable de réponse, ainsi que pour prévoir de nouvelles observations. En règle générale, la régression linéaire utilise la méthode d'estimation par les moindres carrés, qui détermine l'équation en réduisant la somme des valeurs résiduelles mises au carré.
Par exemple, vous travaillez pour un fabricant de pommes chips qui analyse les facteurs affectant le pourcentage de chips brisées par conteneur avant expédition (variable de réponse). Vous effectuez l'analyse de régression et incluez le pourcentage de pomme de terre par rapport aux autres ingrédients et la température de cuisson (Celsius) comme prédicteurs. Le tableau suivant fournit les résultats de l'analyse.
Analyse de régression : Chips brisée en fonction de Pourcentage ; Température
- Pour chaque augmentation de 1 degré Celsius de la température de cuisson, le pourcentage de chips brisées devrait augmenter de 0,022 %.
- Si vous utilisez 50 % (0,5) de pomme de terre et une température de cuisson de 175 °C, la valeur attendue obtenue pour le pourcentage de chips brisées est de 7,7 % : 4,251 - 0,909 * 0,5 + 0,2231 * 175 = 7,70075.
- Le signe de chaque coefficient indique la direction de la relation.
- Les coefficients représentent l'évolution moyenne de la réponse pour un changement d'unité dans le prédicteur, sans modification des autres prédicteurs du modèle.
- La valeur de p de chaque coefficient teste l'hypothèse nulle selon laquelle le coefficient est égal à zéro (aucun effet). Par conséquent, de faibles valeurs de p indiquent que l'ajout du prédicteur au modèle est significatif.
- L'équation prévoit de nouvelles observations, en fonction de valeurs de prédicteur spécifiques.
Remarque
Lorsque les modèles ne comportent qu'un prédicteur, on parle de régression simple. Lorsque les modèles comportent plusieurs prédicteurs, on parle de régression linéaire multiple.
Qu'est-ce qu'une régression linéaire simple ?
La régression linéaire simple examine la relation linéaire entre deux variables continues : une réponse (Y) et un prédicteur (X). Lorsqu'il existe une relation entre les deux variables, il est possible de prévoir une valeur de réponse à partir de la valeur du prédicteur avec une précision améliorée.
- Examiner la façon dont la variable de réponse évolue lorsque la variable de prédiction varie.
- Prédire la valeur d'une variable de réponse (Y) pour n'importe quelle variable de prédiction (X).
Qu'est-ce qu'une régression linéaire multiple ?
La régression linéaire multiple examine les relations linéaires entre une réponse continue et deux prédicteurs ou plus.
Si le nombre des prédicteurs est important, avant d'ajuster un modèle de régression avec tous les prédicteurs, vous devez utiliser la régression pas à pas ou celle sur les meilleurs sous-ensembles pour sélectionner le modèle en éliminant les prédicteurs non associés aux réponses.
Qu'est-ce que la régression sur les moindres carrés ?
Dans la régression sur les moindres carrés, l'équation estimée correspond à l'équation qui minimise la somme des distances quadratiques entre les points de données de l'échantillon et les valeurs prévues par l'équation.
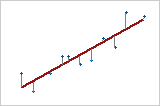
Réponse par rapport à Prédicteur
Avec un prédicteur (régression linéaire simple), la somme des distances quadratiques entre chaque point et la droite est aussi petite que possible.
Hypothèses devant être satisfaites pour la régression sur les moindres carrés
- Le modèle de régression est linéaire pour les coefficients. La méthode par les moindres carrés peut modéliser la courbure en transformant les variables (plutôt que les coefficients). Vous devez spécifier la forme fonctionnelle adéquate afin de modéliser correctement n'importe quelle courbure.
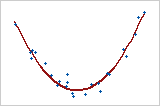
Modèle quadratique
Dans ce cas, la variable de prédiction, X, est élevée au carré afin que la courbure soit modélisée. Y = bo + b1X + b2X2
- La moyenne des valeurs résiduelles est égale à zéro. L'inclusion d'une constante dans le modèle oblige la moyenne à prendre la valeur zéro.
- Aucun prédicteur n'est corrélé aux valeurs résiduelles.
- Les valeurs résiduelles ne sont pas corrélées les unes aux autres (corrélation en série).
- Les valeurs résiduelles présentent une variance constante.
- Aucune variable de prédiction n'est parfaitement corrélée (r=1) à une autre variable de prédiction. Il est également préférable d'éviter les corrélations imparfaitement élevées (multicolinéarité).
- Les valeurs résiduelles ont une distribution normale.
Etant donné que la régression sur les moindres carrés ne fournit les meilleures estimations que lorsque toutes ces hypothèses sont satisfaites, il est extrêmement important de les tester. Parmi les méthodes courantes figurent l'examen des graphiques des valeurs résiduelles, l'utilisation de tests d'inadéquation de l'ajustement et l'affichage de la corrélation entre les prédicteurs à l'aide du facteur d'inflation de la variance (FIV).
