Sur ce thème
Composantes de la variance
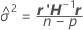
où 

Pour plus de détails sur l'estimation de θi, voir [1].
Pour plus de détails sur la notation, reportez-vous à la rubrique sur les méthodes.
Références
- Hemmerle, W. et Hartley, H. (1973), Computing Maximum Likelihood Estimates for the Mixed A.O.V. Model using the W transformation, Technometrics, 15(4):819–831.
Erreurs types des composantes de la variance
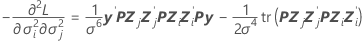
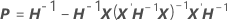
 colonne, j = 1, …, c :
colonne, j = 1, …, c :
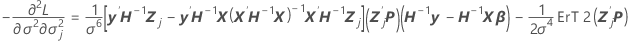

Cette composante est également la valeur de la dernière colonne et de la  ligne par la propriété de symétrie de la matrice de variance/covariance.
ligne par la propriété de symétrie de la matrice de variance/covariance.

La matrice de variance/covariance asymptotique pour les estimations des composantes de variance est égale à deux fois l'inverse de la matrice des informations de Fisher observées. Les estimations des erreurs types sont les racines carrées des éléments se trouvant sur la diagonale de la matrice de variance/covariance. Les c premiers éléments de la diagonale correspondent aux composantes de variance des termes d'effet aléatoire. Le dernier élément de la diagonale correspond à la composante de variance de l'erreur.
Notation
| Terme | Description |
|---|---|
 | trace de la matrice  |
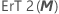 | somme des carrés de tous les éléments de la matrice M |
Pour plus de détails sur la notation, reportez-vous à la rubrique sur les méthodes.
Intervalles de confiance pour les composantes de la variance
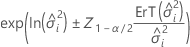
Notation
| Terme | Description |
|---|---|
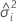 | composante de variance du ie facteur aléatoire |
 | 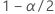 -ième quantile de la loi normale standard -ième quantile de la loi normale standard |
 | 1 - niveau de confiance |
Valeur de Z et valeur de p
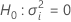
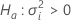


Notation
| Terme | Description |
|---|---|
| Z | valeur de la fonction de répartition inverse pour la loi normale standard |
Matrice de variance/covariance
 composante de la matrice des informations de Fisher :
composante de la matrice des informations de Fisher :
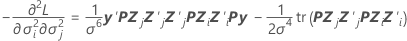

 colonne, j = 1, …, c:
colonne, j = 1, …, c:
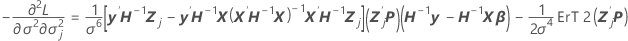

Cette composante est également la valeur de la dernière colonne et de la  ligne par la propriété de symétrie de la matrice de variance/covariance.
ligne par la propriété de symétrie de la matrice de variance/covariance.

Notation
| Terme | Description |
|---|---|
 | trace de la matrice  |
Pour plus de détails sur la notation, reportez-vous à la rubrique sur les méthodes.
