Sur ce thème
Modèle mixte et log de vraisemblance
Forme générale du modèle mixte
Les modèles à effets mixtes contiennent des effets fixes et aléatoires. La forme générale du modèle à effets mixtes est la suivante :
y = Xβ + Z1μ1+ Z2μ2 + ... + Zcμc + ε
Notation
| Terme | Description |
|---|---|
| y | vecteur n x 1 des valeurs de réponse |
| X | matrice de plan n x p pour les effets fixes, p ≤ n |
| Zi | matrice de plan n x mipour le ie effet aléatoire du modèle |
| β | vecteur p x 1 de paramètres inconnus |
| μi | un vecteur mi x 1 de variables indépendantes issus d'une loi N(0, σ2i) |
| ε | vecteur n x 1 de variables indépendantes issues d'une loi N(0, σ2i) |
| c | nombre d'effets aléatoires dans le modèle |
Formes particulières du modèle mixte
L'étude de stabilité ajuste deux modèles avec un facteur de lot aléatoire. Le plus grand modèle contient la durée, le facteur de lot aléatoire et l'interaction aléatoire entre la durée et le lot.
y = Xβ + Z1μ1+ Z2μ2 + ε
Le plus petit modèle contient la durée et le facteur de lot aléatoire.
y = Xβ + Z1μ1+ε
La matrice de variance/covariance générale du vecteur de réponse, y, est définie comme suit :
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
où
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c sont appelés des composantes de la variance.
En factorisant la variance, vous pouvez trouver une représentation de H(θ), qui se trouve dans le calcul du log de vraisemblance des modèles mixtes.
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
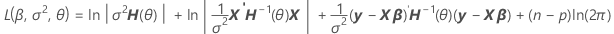
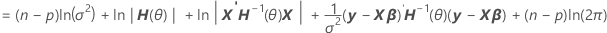
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| p | nombre de paramètres dans β, 2 pour les études de stabilité |
| σ2 | composante de variance pour l'erreur |
| X | matrice de plan pour les termes fixes, la constante et le terme temporel |
| H(θ) | In + θ1Z1Z'1 + ... + θcZcZ'c |
| In | matrice d'identité avec n lignes et colonnes |
| θi | rapport de la variance du ie terme aléatoire sur celle de l'erreur |
| Zi | matrice n x mi des codages connus pour le ie effet aléatoire du modèle |
| mi | nombre de niveaux pour le ie effet aléatoire |
| c | nombre d'effets aléatoires dans le modèle |
| |H(θ)| | déterminant de H(θ) |
| X' | transposition de X |
| H-1(θ) | inverse de H(θ) |
Transformation de Box-Cox
La transformation de Box-Cox sélectionne les valeurs lambda (comme indiqué ci-dessous) qui minimisent la somme des carrés des valeurs résiduelles. La transformation obtenue est Y λ lorsque λ ≠ 0, et ln(Y) lorsque λ = 0. Lorsque λ < 0, Minitab multiplie également la réponse transformée par −1 pour conserver l'ordre de la réponse non transformée.
Minitab recherche une valeur optimale entre −2 et 2. Les valeurs en dehors de cet intervalle sont susceptibles de ne pas fournir un meilleur ajustement.
Voici quelques transformations courantes dans lesquelles Y′ représente la transformation des données Y :
| Valeur lambda (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 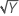 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Sélection du modèle pour un lot aléatoire
- Durée + Lot + Lot*Durée (pentes et ordonnées à l'origine inégales pour les lots)
- Durée + Lot (pentes égales et ordonnées à l'origine inégales pour les lots)
- Durée (pentes et ordonnées à l'origine égales pour les lots)
Si l'interaction Lot*Durée est significative, l'analyse ajuste le premier modèle. Si l'interaction n'est pas significative mais que le terme Lot l'est dans le deuxième modèle, l'analyse ajuste le deuxième modèle. Sinon, l'analyse ajuste le troisième modèle.
Le test permettant de déterminer si les lots doivent être regroupés est légèrement différent de celui qui détermine si le terme Lot doit être inclus, bien que les deux dépendent de la loi du Khi deux. Les formules des statistiques de test et des valeurs de p sont les suivantes.
Test entre le modèle 1 et le modèle 2
différence = −2L2 − (−2L1)
p = 0,5 * Prob(χ21 > différence) + 0,5 * Prob(χ22 > différence)
Test entre le modèle 2 et le modèle 3
différence = −2L3 − (−2L2)
p = 0,5 * Prob(χ21 > différence)
Notation
| Terme | Description |
|---|---|
| La | log de vraisemblance pour le modèle a |
| p | valeur de p du test |
| Prob(χ21 > différence) | probabilité qu'une variable aléatoire suivant une loi du Khi deux à 1 degré de liberté soit supérieure à la différence |
| Prob(χ22 > différence) | probabilité qu'une variable aléatoire suivant une loi du Khi deux à 2 degrés de liberté soit supérieure à la différence |
Références
- Searle, S.R., Casella, G. et McCuloch, C.E. (1992), Variance Components
- West, B.T., Welch, K.B. et Galecki, A.T. (2007), Linear Mixed Models: A Practical Guide Using Statistical Software.
- Chow, S. (2007), Statistical Design and Analysis of Stability Studies.
