Sur ce thème
Valeur ajustée
Valeur prévue de y, ou 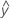 , qui est la valeur de réponse moyenne pour les valeurs de prédicteur données, d'après l'équation de régression estimée.
, qui est la valeur de réponse moyenne pour les valeurs de prédicteur données, d'après l'équation de régression estimée.
Erreur type de la valeur ajustée marginale (Ajust ErT)
L'erreur type des valeurs ajustées marginales dans le modèle mixte dépend de la méthode de test utilisée pour les effets fixes. Pour les deux méthodes, les erreurs types sont les racines carrées des éléments se trouvant sur la diagonale de la matrice de variance des valeurs ajustées.
Méthode de Kenward-Roger

où
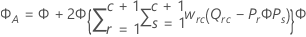
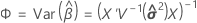
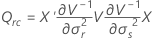
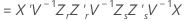
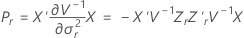
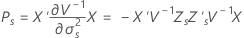
Approximation de Satterthwaite

où
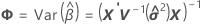
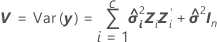
Valeurs résiduelles
Une valeur résiduelle est la différence entre une valeur observée et une valeur ajustée. Elle représente la part de l'observation non expliquée par le modèle ajusté. La valeur résiduelle d'une observation est obtenue comme suit :
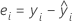
Lorsque le lot est un facteur aléatoire, Minitab calcule 2 types de valeurs résiduelles. Les valeurs résiduelles marginales utilisent la valeur ajustée correspondant à un lot aléatoire, de sorte que le coefficient du lot n'est pas dans l'équation.
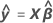
Les valeurs résiduelles conditionnelles utilisent les valeurs ajustées d'un lot inclus dans les données.
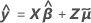
Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
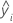 | ie valeur de réponse ajustée |
 | vecteur des réponses ajustées |
| X | matrice de plan pour les effets fixes |
 | vecteur des prédicteurs fixes |
| Z | matrice de plan pour les facteurs aléatoires |
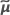 | vecteur des valeurs BLUP estimées |
Valeurs résiduelles normalisées

où l'écart type de la valeur résiduelle est la racine carrée de la diagnoale correspondante de la matrice de variance résiduelle :
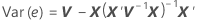
où
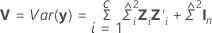
Notation
| Terme | Description |
|---|---|
| ei | ie valeur résiduelle |
| EcTyp(ei) | écart type de la ie valeur résiduelle |
Intervalle de confiance
Etendue de valeurs dans laquelle la réponse moyenne estimée d'un ensemble de valeurs de prédicteurs devrait se trouver.


où
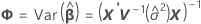
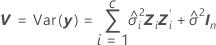
Les degrés de liberté peuvent être obtenus par la formule suivante lorsque le lot est un facteur aléatoire :
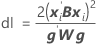
où

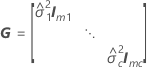
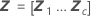
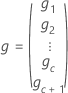

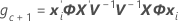
Notation
| Terme | Description |
|---|---|
| t1-α/2, dl | Quantile 1–α/2 de la loi t avec le nombre de degrés de liberté donné |
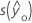 | erreur type de la valeur ajustée |
| X | matrice du plan, contenant la constante |
| X' | transposition de X |
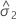 | composante de variance pour l'erreur |
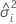 | composante de variance pour le ie facteur aléatoire |
| Zi | matrice n x mi des codages connus pour le ie effet aléatoire du modèle |
| Zi' | transposition de Zi |
| In | matrice d'identité avec n lignes et colonnes |
| xi | valeurs de prédicteur pour l'ajustement ou la prévision |
| W | matrice de variance/covariance asymptotique de la composante de variance pour l'erreur |
| c | nombre d'effets aléatoires dans le modèle |
Intervalle de prévision
Etendue de valeurs dans laquelle la réponse prévue pour une nouvelle observation a de fortes chances de se trouver. Le calcul de l'intervalle de prévision dépend de l'ajustement étudié : l'ajustement marginal ou l'ajustement conditionnel.
Ajustement marginal

où
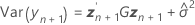

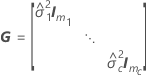
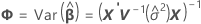
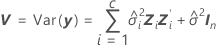
Les degrés de liberté pour la statistique t sont obtenus avec la formule suivante :
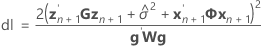
où
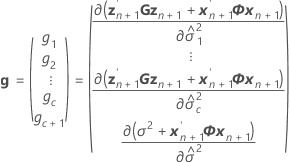


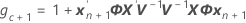
Ajustement conditionnel

où
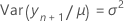
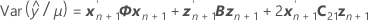
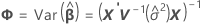
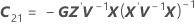
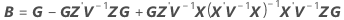
Les degrés de liberté pour la statistique t sont calculés comme suit :
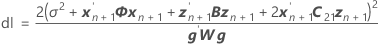
où
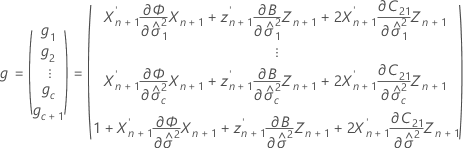

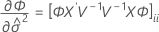
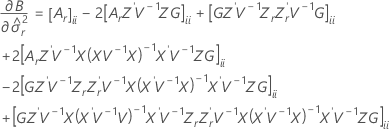
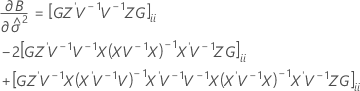
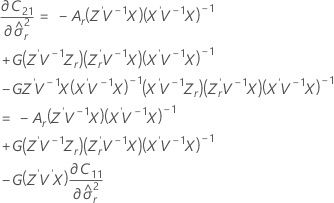
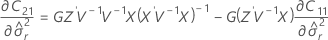
Notation
| Terme | Description |
|---|---|
 | Quantile 1–α/2 de la loi t avec le nombre de degrés de liberté donné |
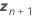 | vecteur des nouvelles valeurs des prédicteurs aléatoires |
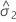 | composante de variance pour l'erreur |
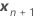 | vecteur des nouvelles valeurs des prédicteurs fixes |
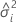 | composante de variance pour le ie facteur aléatoire |
| Im | matrice d'identité avec m lignes et colonnes |
| m | nombre de colonnes dans la matrice de plan pour représenter le ie terme aléatoire du modèle |
| c | nombre d'effets aléatoires dans le modèle |
| Zi | matrice de plan n x mi pour le ie effet aléatoire du modèle |
| Z'i | transposition de Zi |
