Sur ce thème
Coefficients dans les modèles mixtes
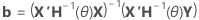
Notation
| Terme | Description |
|---|---|
| X | matrice du plan, contenant la constante |
| X' | transposition de X |
| Y | données de réponse |
 | inverse de  |
 |
 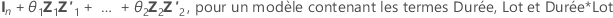  |
 | matrice d'identité avec n lignes et colonnes |
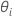 | rapport des variances pour le ie effet aléatoire du modèle |
 | matrice n x mi des codages connus pour le ie effet aléatoire du modèle |
| mi | nombre de niveaux pour le ie effet aléatoire |
| c | nombre d'effets aléatoires dans le modèle c = 2 pour le modèle contenant les termes Durée et Lot, ainsi que l'interaction Durée*Lot c = 1 pour le modèle contenant les termes Durée et Lot |
Erreurs types des coefficients dans les modèles mixtes
Les erreurs types des coefficients dépendent de la méthode de test utilisée pour les effets fixes. Pour plus de détails sur la notation, reportez-vous aux rubriques sur les méthodes et sur les tests des effets fixes.
Approximation de Kenward-Roger
Les erreurs types des coefficients estimés sont les racines carrées des éléments de la diagonale de la matrice suivante 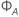 .
.
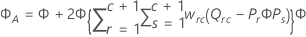
où

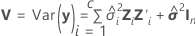
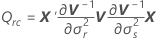
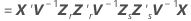
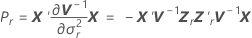
Approximation de Satterthwaite
 .
.

où
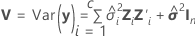
Degrés de liberté pour les coefficients
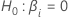
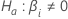
 coefficient :
coefficient :


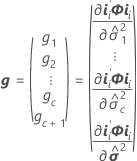

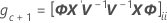
Pour plus de détails sur la notation, reportez-vous aux rubriques sur les méthodes et sur les tests des effets fixes.
Intervalles de confiance pour les coefficients
 coefficient correspondent à l'équation suivante :
coefficient correspondent à l'équation suivante :

Notation
| Terme | Description |
|---|---|
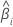 | coefficient estimé |
 | (1 − α/2)-ième percentile de la loi T avec dl degrés de liberté |
 | erreur type du coefficient estimé |
Valeur de t

Notation
| Terme | Description |
|---|---|
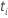 | statistique de test pour l' coefficient coefficient |
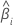 |  coefficient estimé coefficient estimé |
 | erreur type de l'  coefficient estimé coefficient estimé |
Valeur de p (P)
L'équation suivante donne la valeur de p bilatérale pour l'hypothèse nulle selon laquelle un coefficient est égal à 0 :

Notation
| Terme | Description |
|---|---|
 | Probabilité que, sous l'hypothèse nulle, T soit inférieur à la valeur absolue de 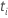 calculée. Ici, T suit une loi T avec dl degrés de liberté. calculée. Ici, T suit une loi T avec dl degrés de liberté. |
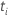 | Valeur de t pour l' coefficient. coefficient. |
