Sur ce thème
- Etape 1 : Déterminer si l'association entre la réponse et le terme est statistiquement significative
- Etape 2 : Déterminer la durée de stockage du produit
- Etape 3 : Etudier la relation entre le terme et la réponse
- Etape 4 : Déterminer l'ajustement du modèle à vos données
- Etape 5 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Etape 1 : Déterminer si l'association entre la réponse et le terme est statistiquement significative
Si vos données contiennent un facteur de lot, le tableau de sélection de modèle présente les résultats du processus de sélection. Minitab utilise le modèle final issu du processus de sélection pour estimer la durée de stockage.
Minitab part du modèle complet, qui comprend les termes Durée, Lot et l'interaction entre la durée et le lot. Minitab compare ensuite la valeur de p de l'interaction au seuil défini dans Alpha pour le regroupement des lots (aussi appelé α). Si la valeur de p de l'interaction est inférieure à α, le modèle ne peut pas être réduit. Le modèle final inclut les trois termes.
Si la valeur de p de l'interaction est supérieure ou égale à α, Minitab enlève l'interaction et évalue le modèle réduit comportant uniquement le lot et la durée. Si la valeur de p du lot dans le modèle réduit est inférieure à α, le modèle ne peut plus être réduit. Le modèle final inclut le lot et la durée.
Si la valeur de p du lot dans le modèle réduit est supérieure ou égale à α, Minitab enlève le lot. Le modèle final inclut uniquement la durée.
Sélection du modèle avec α = 0,25
| Source | DL | SomCar séq | CM séq | Valeur F | Valeur de p |
|---|---|---|---|---|---|
| Mois | 1 | 122,460 | 122,460 | 345,93 | 0,000 |
| Lot | 4 | 2,587 | 0,647 | 1,83 | 0,150 |
| Mois*Lot | 4 | 3,850 | 0,962 | 2,72 | 0,048 |
| Erreur | 30 | 10,620 | 0,354 | ||
| Total | 39 | 139,516 |
Résultats principaux : valeur de p
Dans cet exemple avec un facteur de lot fixe, la valeur de p de l'interaction Mois*Lot est de 0,048. Cette valeur de p étant inférieure au seuil de signification de 0,25, les pentes sont différentes pour les équations de régression de chaque lot.
Etape 2 : Déterminer la durée de stockage du produit
Le tableau d'estimation de la durée de stockage indique les limites de spécification, le niveau de confiance utilisé pour calculer la durée de stockage, ainsi que les estimations de la durée de stockage.
Si le facteur de lot est fixe et n'est pas compris dans le modèle final, la durée de stockage est la même pour tous les lots. Sinon, la durée de stockage est différente pour tous les lots et Minitab affiche l'estimation de la durée de stockage pour chacun d'entre eux. La durée de stockage globale pour le produit est égale à la plus petite durée de stockage individuelle.
Si le facteur de lot est aléatoire, Minitab calcule uniquement la durée de stockage globale.
Estimation de la durée de stockage
Durée de stockage = durée pendant laquelle vous pouvez être sûr à 95 % qu'au moins 50 % de la
réponse se trouvent au-dessus de la limite de spécification inférieure
| Lot | Durée de stockage |
|---|---|
| 1 | 83,552 |
| 2 | 54,790 |
| 3 | 57,492 |
| 4 | 60,898 |
| 5 | 66,854 |
| Global | 54,790 |
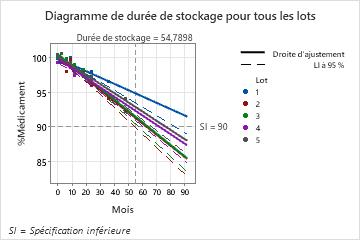
Résultats principaux : estimations de la durée de stockage, diagramme de durée de stockage
Dans ces résultats, le modèle final inclut le facteur de lot et Minitab affiche donc les estimations de la durée de stockage pour chaque lot. La durée de stockage globale estimée est de 54,79 mois. Cette valeur correspond à la durée de stockage du lot 2, qui est la plus courte.
Etape 3 : Etudier la relation entre le terme et la réponse
Pour un facteur de lot fixe, si la durée est le seul terme compris dans le modèle final, tous les lots partagent la même ordonnée à l'origine et la même pente, et Minitab n'affiche qu'une seule équation de régression. Sinon, Minitab affiche une équation distincte pour chaque lot. Si le facteur de lot est inclus dans le modèle final, mais pas l'interaction entre la durée et le lot, les lots ont tous une ordonnée à l'origine différente mais présentent la même vitesse de dégradation. Si le facteur de lot et l'interaction entre la durée et le lot sont tous deux inclus dans le modèle final, les lots ont tous une ordonnée à l'origine et une pente différentes.
Equation de régression
| Lot | |||
|---|---|---|---|
| 1 | %Médicament | = | 99,853 - 0,0909 Mois |
| 2 | %Médicament | = | 100,153 - 0,1605 Mois |
| 3 | %Médicament | = | 100,479 - 0,1630 Mois |
| 4 | %Médicament | = | 99,769 - 0,1350 Mois |
| 5 | %Médicament | = | 100,173 - 0,1323 Mois |
Résultats principaux : équation de régression
Dans ces résultats, le terme Mois et l'interaction Mois*Lot sont tous les deux significatifs. Par conséquent, les équations de régression de chaque lot ont des ordonnées à l'origine et des pentes différentes. Le lot 3 est celui dont la pente est la plus forte, −0,1630, ce qui indique que la concentration du médicament (%Médicament) dans le lot 3 diminue chaque mois de 0,163 point de pourcentage. Le lot 4 est celui qui a la plus petite ordonnée à l'origine, 99,769, ce qui signifie que c'est celui qui présente la plus faible concentration au moment 0.
Etape 4 : Déterminer l'ajustement du modèle à vos données
Pour déterminer l'ajustement du modèle aux données, étudiez les statistiques d'adéquation de l'ajustement dans le tableau Récapitulatif du modèle.
- R carré
-
R2 représente le pourcentage de variation de la réponse expliqué par le modèle. Plus la valeur R2 est élevée, plus le modèle est ajusté à vos données. R2 est toujours compris entre 0 et 100 %.
La valeur R2 augmente toujours lorsque vous ajoutez des prédicteurs à un modèle. Par exemple, le meilleur modèle à 5 prédicteurs aura toujours une valeur R2 au moins aussi élevée que celle du meilleur modèle à 4 prédicteurs. Par conséquent, R2 est surtout utile pour comparer des modèles de même taille.
- R carré (ajusté)
-
Utilisez la valeur R2 ajusté pour comparer des modèles n'ayant pas le même nombre de prédicteurs. R2 augmente toujours lorsque vous ajoutez un prédicteur au modèle, même lorsque ce prédicteur n'apporte aucune amélioration réelle au modèle. La valeur de R2 ajusté intègre le nombre de prédicteurs dans le modèle pour vous aider à choisir le modèle correct.
-
Les petits échantillons ne fournissent pas d'estimation précise de la force de la relation entre la réponse et les prédicteurs. Par exemple, pour obtenir une valeur R2 plus précise, vous devez utiliser un échantillon plus grand (en général, 40 ou plus).
-
Les statistiques d'adéquation de l'ajustement ne sont qu'un des types de mesures permettant d'évaluer l'ajustement du modèle. Même si un modèle a une valeur souhaitable, vous devez consulter les graphiques des valeurs résiduelles pour vérifier que le modèle respecte les hypothèses.
Récapitulatif du modèle
| S | R carré | R carré (ajust) | R carré (prév) |
|---|---|---|---|
| 0,594983 | 92,39% | 90,10% | 85,22% |
Résultats principaux : R carré
Dans ces résultats, le R2 le R2 ajusté sont proches de 100, ce qui indique que le modèle est bien ajusté aux données.
Etape 5 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Les graphiques des valeurs résiduelles permettent de déterminer si le modèle est adapté et si les hypothèses de l'analyse sont vérifiées. Si elles ne le sont pas, il se peut que le modèle ne soit pas ajusté aux données et vous devez être prudent lors de l'interprétation des résultats.
Remarque
Si votre modèle inclut un facteur de lot aléatoire, vous pouvez créer un graphique représentant les valeurs résiduelles marginales et conditionnelles. Les valeurs ajustées marginales sont les valeurs ajustées pour la population globale. Les valeurs résiduelles conditionnelles permettent de vérifier la normalité du terme d'erreur dans le modèle.
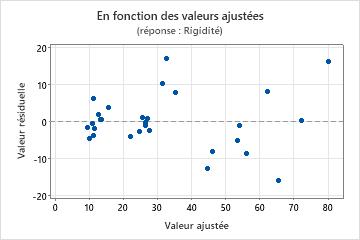
Graphique des valeurs résiduelles en fonction des valeurs ajustées
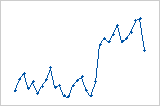
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles suivent une loi normale et ont une variance constante. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Curviligne | Un terme d'ordre supérieur manquant |
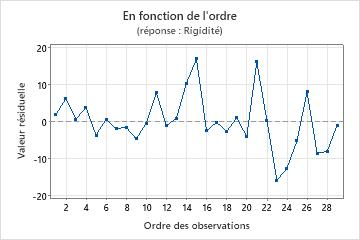
| Un point très éloigné de zéro | Une valeur aberrante |
| Un point éloigné des autres points dans le sens des x | Un point influent |
Graphique des valeurs résiduelles en fonction de l'ordre
Tendance
Equipe
Cycle
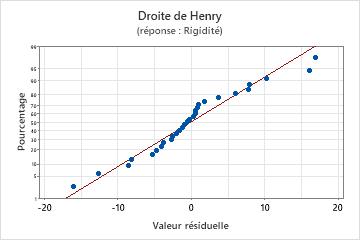
Droite de Henry
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
| Schéma | Ce que le schéma indique |
|---|---|
| Une ligne qui n'est pas droite | Non-normalité |
| Un point éloigné de la ligne | Une valeur aberrante |
| Une modification de la pente | Une variable non identifiée |
Pour plus d'informations sur la manière de traiter les schémas dans les graphiques des valeurs résiduelles, reportez-vous à la rubrique Graphiques des valeurs résiduelles pour la fonction Droite d'ajustement.
