Sélectionner le modèle
Un ingénieur qualité travaillant pour un fabricant de médicaments souhaite déterminer la durée de stockage maximale d'un médicament. La concentration de l’ingrédient actif dans le médicament diminue avec le temps. L’ingénieur veut déterminer quand la concentration atteint 90 % de la concentration prévue. L’ingénieur sélectionne au hasard 8 lots de médicaments parmi une plus grande population de lots possibles et teste un échantillon de chaque lot à neuf moments différents.
Pour estimer la durée de stockage, l'ingénieur effectue une étude de stabilité. Étant donné que les lots sont un échantillon aléatoire à partir d’une plus grande population de lots possibles, le lot est un facteur aléatoire au lieu d’un facteur fixe.
- Ouvrez l’exemple de données DuréeStockageAléatoireLots.MWX.
- Choisissez .
- Sélectionnez Le lot est un facteur aléatoire (modèle mixte).
- Dans Réponse, saisissez %Médicament.
- Dans Durée, saisissez Mois.
- Dans Lot, saisissez Lot.
- Dans Spécification inférieure, saisissez 90.
- Cliquez sur Graphiques.
- Sous Graphiques des valeurs résiduelles, sélectionnez Quatre en un.
- Cliquez sur OK dans chaque boîte de dialogue
Interpréter des résultats
La valeur p qui compare les modèles avec et sans l’interaction Mois par lot est de 0,059. Étant donné que la valeur p est inférieure au niveau de signification de 0,25, l’analyse utilise le modèle avec l’interaction Mois par lot. La durée de conservation, qui est d’environ 53 mois, est une estimation de la durée pendant laquelle l’ingénieur peut être sûr à 95 % que 95 % du médicament est au-dessus de la limite inférieure des spécifications. L’estimation s’applique à tout lot que l’ingénieur sélectionne au hasard dans le processus.
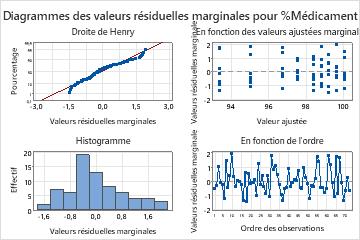
Les résidus marginaux peuvent ne pas suivre une distribution normale à variance constante. Les points du graphique de probabilité normale ne suivent pas bien la droite. L’une des raisons du comportement non normal des résidus marginaux est que, lorsque le modèle final inclut l’interaction lot-temps, la variance des résidus marginaux dépend de la variable temporelle et peut ne pas être constante. Vous pouvez utiliser les valeurs résiduelles conditionnelles pour vérifier la normalité du terme d'erreur dans le modèle.
Informations sur les facteurs
| Facteur | Type | Nombre de niveaux | Niveaux |
|---|---|---|---|
| Lot | Aléatoire | 8 | 1; 2; 3; 4; 5; 6; 7; 8 |
Sélection du modèle avec α = 0,25
| Modèle | Log de vraisemblance -2 | Différence | Valeur de p |
|---|---|---|---|
| Mois Lot Mois*Lot | 128,599 | ||
| Mois Lot | 133,424 | 4,82476 | 0,059 |
Composantes de la variance
| Source | Var | % du total | Var. ErT | Valeur de Z | Valeur de p |
|---|---|---|---|---|---|
| Lot | 0,527409 | 72,91% | 0,303853 | 1,735739 | 0,041 |
| Mois*Lot | 0,000174 | 0,02% | 0,000142 | 1,224102 | 0,110 |
| Erreur | 0,195739 | 27,06% | 0,036752 | 5,325932 | 0,000 |
| Total | 0,723322 |
Récapitulatif du modèle
| S | R carré | R carré (ajust) |
|---|---|---|
| 0,442424 | 96,91% | 96,87% |
Coefficients
| Terme | Coeff | Coef ErT | DL | Valeur de T | Valeur de p |
|---|---|---|---|---|---|
| Constante | 100,060247 | 0,268706 | 7,22 | 372,378347 | 0,000 |
| Mois | -0,138766 | 0,005794 | 7,22 | -23,950196 | 0,000 |
Prévisions des effets aléatoires
| Terme | BLUP | EcTyp | DL | Valeur de T | Valeur de p |
|---|---|---|---|---|---|
| Lot | |||||
| 1 | 1,359433 | 0,313988 | 12,45 | 4,329567 | 0,001 |
| 2 | 0,395375 | 0,313988 | 12,45 | 1,259203 | 0,231 |
| 3 | 0,109151 | 0,313988 | 12,45 | 0,347629 | 0,734 |
| 4 | -0,409322 | 0,313988 | 12,45 | -1,303623 | 0,216 |
| 5 | -0,135643 | 0,313988 | 12,45 | -0,432001 | 0,673 |
| 6 | -1,064736 | 0,313988 | 12,45 | -3,391006 | 0,005 |
| 7 | 0,049420 | 0,313988 | 12,45 | 0,157394 | 0,877 |
| 8 | -0,303678 | 0,313988 | 12,45 | -0,967164 | 0,352 |
| Mois*Lot | |||||
| 1 | 0,006281 | 0,008581 | 10,49 | 0,731925 | 0,480 |
| 2 | 0,019905 | 0,008581 | 10,49 | 2,319537 | 0,042 |
| 3 | -0,013831 | 0,008581 | 10,49 | -1,611742 | 0,137 |
| 4 | 0,003468 | 0,008581 | 10,49 | 0,404173 | 0,694 |
| 5 | 0,001240 | 0,008581 | 10,49 | 0,144455 | 0,888 |
| 6 | 0,000276 | 0,008581 | 10,49 | 0,032144 | 0,975 |
| 7 | -0,010961 | 0,008581 | 10,49 | -1,277272 | 0,229 |
| 8 | -0,006378 | 0,008581 | 10,49 | -0,743220 | 0,474 |
Ajustements et diagnostics marginaux pour les observations aberrantes
| Observation | %Médicament | Valeur ajustée | DL | Résiduelle | Val. résid. norm. | |
|---|---|---|---|---|---|---|
| 10 | 101,564000 | 99,643950 | 7,04368 | 1,920050 | 2,375254 | R |
| 31 | 100,618000 | 98,811354 | 7,05273 | 1,806646 | 2,213787 | R |
| 55 | 98,481000 | 96,729866 | 8,87383 | 1,751134 | 2,033482 | R |
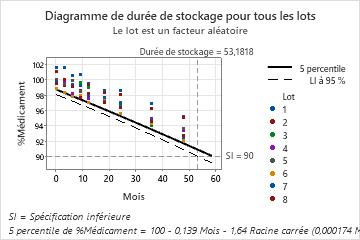
Estimation de la durée de stockage
Durée de stockage = durée pendant laquelle vous pouvez être sûr à 95 % qu'au moins 95 % de la
réponse se trouvent au-dessus de la limite de spécification inférieure
Durée de stockage pour tous les lots = 53,1818
Vérifier les valeurs résiduelles conditionnelles
- Sélectionnez .
- Cliquez sur Graphiques.
- Dans Valeurs résiduelles des graphiques, sélectionnez Conditionnel, standard.
- Cliquez sur OK dans chaque boîte de dialogue.
Interprétation des résultats
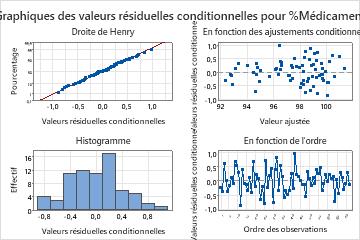
Dans ces résultats, les valeurs résiduelles conditionnelles suivent visiblement une loi normale. Le modèle complet semble correctement ajusté aux données.
