Exemple de la fonction Etude de stabilité avec un facteur de lot fixe

Un ingénieur qualité travaillant pour un laboratoire pharmaceutique souhaite déterminer la durée de stockage maximale de pilules contenant un nouveau médicament. La concentration du médicament dans les pilules diminue au fil du temps. L'ingénieur souhaite déterminer le moment où la concentration des pilules tombe à 90 % de la concentration souhaitée. Comme il s'agit d'un nouveau médicament, l'entreprise ne dispose que de 5 lots pilotes à utiliser pour estimer la durée de stockage. L'ingénieur teste une pilule pour chaque lot, à neuf moments différents.

Pour estimer la durée de stockage, l'ingénieur effectue une étude de stabilité. L'ingénieur échantillonnant tous les lots, le lot est un facteur fixe et non un facteur aléatoire.

Ouvrez les données échantillons, DuréeStockage.MTW.
Sélectionnez Stat > Régression > Etude de stabilité > Etude de stabilité.
Dans la zone Réponse, saisissez %Médicament.
Dans la zone Durée, saisissez Mois.
Dans la zone Lot, saisissez Lot.
Dans la zone Spécification inférieure, saisissez 90.
Cliquez sur Graphiques.
Sous Diagramme de durée de stockage, dans la deuxième liste déroulante, sélectionnez Pas de graphique pour les lots individuels.
Sous Graphiques des valeurs résiduelles, sélectionnez Quatre en un.
Cliquez sur OK dans chaque boîte de dialogue

Interpréter des résultats

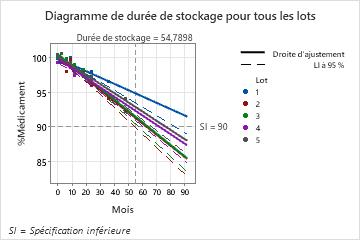
Pour se conformer aux recommandations de 2003 de la conférence internationale sur l'harmonisation des exigences techniques pour l'enregistrement des médicaments à usage humain (CIH), l'ingénieur sélectionne une valeur de p de 0,25 pour les termes à inclure dans le modèle. La valeur de p pour l'interaction Mois*Lot est de 0,048. Cette valeur de p étant inférieure au seuil de signification de 0,25, l'ingénieur conclut que les pentes sont différentes pour les équations de régression de chaque lot. Le lot 3 est celui qui présente la plus forte pente, -0,1630, ce qui indique que la concentration décroît plus rapidement dans ce lot. Le lot 2 étant celui qui présente la plus courte durée de stockage, 54,79, la durée de stockage globale est alignée sur celle du lot 2.

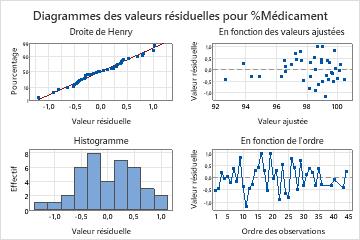
Les valeurs résiduelles présentent une normalité satisfaisante et sont dispersées de façon aléatoire autour de 0. Sur le diagramme des valeurs résiduelles en fonction des valeurs ajustées, on observe un plus petit nombre de points sur le côté gauche que sur le côté droit. Cette disposition est due au fait que l'ingénieur qualité a collecté davantage de données au début de l'étude, quand les concentrations étaient élevées. Elle ne contredit pas les hypothèses de l'analyse.

Source	DL	SomCar séq	CM séq	Valeur F	Valeur de p
Mois	1	122,460	122,460	345,93	0,000
Lot	4	2,587	0,647	1,83	0,150
Mois*Lot	4	3,850	0,962	2,72	0,048
Erreur	30	10,620	0,354
Total	39	139,516

Terme	Coeff	Coef ErT	Valeur de T	Valeur de p	FIV
Constante	100,085	0,143	701,82	0,000
Mois	-0,13633	0,00769	-17,74	0,000	1,07
Lot
1	-0,232	0,292	-0,80	0,432	3,85
2	0,068	0,292	0,23	0,818	3,85
3	0,394	0,275	1,43	0,162	3,41
4	-0,317	0,292	-1,08	0,287	3,85
5	0,088	0,275	0,32	0,752	*
Mois*Lot
1	0,0454	0,0164	2,76	0,010	4,52
2	-0,0241	0,0164	-1,47	0,152	4,52
3	-0,0267	0,0136	-1,96	0,060	3,65
4	0,0014	0,0164	0,08	0,935	4,52
5	0,0040	0,0136	0,30	0,769	*

Observation	%Médicament	Valeur ajustée	Résiduelle	Val. résid. norm.
11	98,001	99,190	-1,189	-2,21	R
43	92,242	92,655	-0,413	-1,47		X
44	94,069	93,823	0,246	0,87		X

Lot	Durée de stockage
1	83,552
2	54,790
3	57,492
4	60,898
5	66,854
Global	54,790

Exemple de la fonction Etude de stabilité avec un facteur de lot fixe

Interpréter des résultats

Méthode

Informations sur les facteurs

Sélection du modèle avec α = 0,25

Récapitulatif du modèle

Coefficients

Equation de régression

Ajustements et diagnostics pour les observations aberrantes

Estimation de la durée de stockage

Lot
1	%Médicament	=	99,853 - 0,0909 Mois

2	%Médicament	=	100,153 - 0,1605 Mois

3	%Médicament	=	100,479 - 0,1630 Mois

4	%Médicament	=	99,769 - 0,1350 Mois

5	%Médicament	=	100,173 - 0,1323 Mois