Sur ce thème
Coefficients et coefficients normalisés
Les coefficients représentent les paramètres d'une équation de régression. Les coefficients estimés sont utilisés avec les prédicteurs pour calculer la valeur ajustée de la variable de réponse et la réponse prévue des nouvelles observations. A l'inverse des moindres carrés, les coefficients PLS sont des estimateurs non linéaires. Les coefficients normalisés indiquent l'importance de chaque prédicteur dans le modèle et correspondent aux variables X et Y normalisées. Dans PLS, la matrice des coefficients (dimension p × r) est calculée à partir des pondérations et des contributions.
La formule des coefficients normalisés est la suivante :

Pour calculer les coefficients non normalisés et l'ordonnée à l'origine, utilisez les formules suivantes :
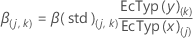

Notation
| Terme | Description |
|---|---|
| W | matrice de pondérations X |
| P | matrice de contributions X |
| C | matrice de contributions Y |
| j | prédicteurs (1, p) |
| k | réponses (1, r) |
| p | nombre de prédicteurs |
| r | nombre de réponses |
Effets de levier
Dans la régression des moindres carrés, les effets de levier sont des valeurs qui indiquent à quelle distance les observations correspondantes se situent par rapport au centre de l'espace X, qui est décrit par les valeurs X. Dans PLS, les prédicteurs sont remplacés par des scores X. Les observations avec un effet de levier important possèdent des scores X éloignés de zéro et ont une incidence significative sur les coefficients de régression. Les points possédant un effet de levier important sont des valeurs aberrantes dans l'espace X, mais pas nécessairement dans l'espace Y.
Les valeurs d'effets de levier dans PLS sont calculées à partir du T de la matrice des scores X, qui sert à calculer la matrice chapeau (H) comme suit :

L'effet de levier (hii) de la ie observation constitue le ie élément diagonal de la matrice H.
Une valeur d'effet de levier supérieure à 2m/n est considérée comme élevée et doit être examinée.
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| m | nombre de composantes |
Distances par rapport au modèle X
Mesure du degré d'ajustement des observations dans l'espace X qui permet d'évaluer la description des observations par les scores X. Une observation possédant une distance importante peut également être un point d'effet de levier.
Formule
La formule du calcul de la distance à partir du modèle X pour la ie observation est la suivante :
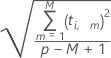
Notation
| Terme | Description |
|---|---|
| M | nombre de composants |
| t | score X |
| p | nombre de prédicteurs |
Distances par rapport au modèle Y
Mesure du degré d'ajustement des observations dans l'espace Y qui permet d'évaluer la description des observations par les scores Y. Une observation possédant une distance importante peut également être une valeur aberrante.
Formule
La formule du calcul de la distance à partir du modèle Y pour la ie observation est la suivante :
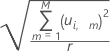
Notation
| Terme | Description |
|---|---|
| M | nombre de composantes |
| u | score Y |
| r | nombre de réponses |
