Sur ce thème
Valeurs ajustées
Y prévu ou 
est la valeur de réponse moyenne pour les valeurs de prédicteurs concernées, obtenue à l'aide de l'équation de régression estimée.
Valeurs ajustées à validation croisée
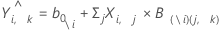
Notation
| Terme | Description |
|---|---|
| \i | Indique que l'observation i a été exclue du calcul du modèle |
| b0\i | ordonnée à l'origine du modèle qui n'inclut pas l'observation i |
| X | valeurs du prédicteur |
| B(\i)(j, k) | coefficients du modèle qui n'inclut pas d'observation i |
Valeurs résiduelles
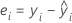
Notation
| Terme | Description |
|---|---|
| yi | ie valeur de réponse observée |
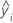 | ie valeur ajustée pour la réponse |
Valeurs résiduelles à validation croisée
Les valeurs résiduelles à validation croisée mesurent la capacité de prévision du modèle et servent à calculer la statistique SomCar-ErrPrév. Les valeurs résiduelles à validation croisée dans la régression PLS et des moindres carrés sont conceptuellement similaires, mais leurs calculs diffèrent.
Formule
Dans PLS, les valeurs résiduelles à validation croisée sont les différences entre les réponses réelles et les valeurs ajustées à validation croisée.
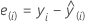
La valeur résiduelle à validation croisée varie selon le nombre d'observations omises à chaque nouveau calcul du modèle lors de la validation croisée.
Dans la régression des moindres carrés, les valeurs résiduelles à validation croisée sont calculées directement à partir des valeurs résiduelles ordinaires.
Notation
| Terme | Description |
|---|---|
| (i) | observation omise du calcul du modèle |
| yi | valeur de réponse |
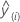 | valeur ajustée à validation croisée |
Valeur résiduelle normalisée (Val. résid. norm)
Les valeurs résiduelles normalisées sont également appelées "valeurs résiduelles studentisées en interne".
Formule
Notation
| Terme | Description |
|---|---|
| ei | ie valeur résiduelle |
| hi | ie élément sur la diagonale de X(X'X)–1X' |
| s2 | carré moyen de l'erreur |
| X | matrice du plan |
| X' | transposition de la matrice de plan |
Erreur type de la valeur ajustée (ErT ajust)
L'erreur type de la valeur ajustée dans un modèle de régression avec un prédicteur est calculée comme suit :
L'erreur type de la valeur ajustée dans un modèle de régression avec plusieurs prédicteurs est calculée comme suit :
Pour la régression pondérée, inclure la matrice de poids dans l’équation:
Lorsque les données disposent d’un ensemble de données de test ou d’une validation croisée Buplé, les formules sont les mêmes. La valeur de s2 provient des données de formation. La matrice de conception et la matrice de poids proviennent également des données de formation.
Notation
| Terme | Description |
|---|---|
| s2 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xi | ie predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| X0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
Intervalle de confiance
L'intervalle de confiance est l'étendue dans laquelle on s'attend à trouver la réponse moyenne estimée d'un ensemble donné de valeurs de prédicteurs. L'intervalle est défini par une limite inférieure et une limite supérieure, calculées par Minitab à partir du niveau de confiance et de l'erreur type des valeurs ajustées.
Formule
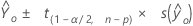
Notation
| Terme | Description |
|---|---|
| α | valeur alpha |
| n | nombre d'observations |
| p | nombre de prédicteurs |
 |  |
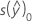| s2 | carré moyen de l'erreur |
| S2(b) | matrice de variance/covariance des coefficients |
Intervalle de prévision
L'intervalle de prévision est l'étendue dans laquelle on s'attend à trouver la réponse ajustée pour une nouvelle observation.
Formule
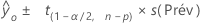
Notation
| Terme | Description |
|---|---|
| s(Prév) |  |
 | valeur de réponse ajustée pour un ensemble donné de valeurs de prédicteurs |
| α | seuil de signification |
| n | nombre d'observations |
| p | nombre de paramètres de modèle |
| s 2 | carré moyen de l'erreur |
| X | matrice de prédicteur |
| X0 | vecteur de valeurs de prédiction données avec une colonne et p lignes |
| X'0 | transposition du nouveau vecteur des valeurs de prédiction avec une ligne et p colonnes |
