Sur ce thème
Scores X
Les scores X sont des combinaisons linéaires de termes, semblables aux scores principaux de composantes. Les scores Y forment une matrice n × m des colonnes non corrélées. Les scores X sont des projections des observations des composantes PLS. PLS ajuste les scores X, qui remplacent les termes d'origine dans les données, suivant l'estimation des moindres carrés.
Formule
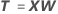
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| m | nombre de composantes |
| i | observations de 1 à n |
| j | termes de 1 à p |
| X | matrice de plan |
| W | matrice de pondération X |
Contributions X
Les contributions X sont des coefficients linéaires qui lient les termes aux scores X ; elles sont semblables aux vecteurs propres dans l'analyse des composantes principales. Les valeurs de contribution indiquent l'importance du terme correspondant pour la me composante. Les contributions X forment une matrice p × m.
Formule
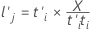
Notation
| Terme | Description |
|---|---|
| p | nombre de termes |
| m | nombre de composantes |
| i | observations de 1 à n |
| j | termes de 1 à p |
| t | scores X |
| X | prédicteurs |
Pondérations X
Les pondérations X décrivent la covariance entre les termes et les réponses. Dans l'algorithme, les pondérations permettent de faire en sorte que les scores X soient orthogonaux ou non liés les uns aux autres ; elles servent aussi à calculer les scores X. Les pondérations X forment une matrice p × m.
Formule
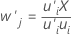
Minitab met à l'échelle le vecteur des pondérations afin que sa longueur soit égale à 1.
Notation
| Terme | Description |
|---|---|
| p | nombre de termes |
| m | nombre de composantes |
| i | observations de 1 à n |
| j | termes de 1 à p |
| X | matrice des valeurs résiduelles X |
| u | scores Y |
Valeurs résiduelles X
Les valeurs résiduelles X contiennent la variance des prédicteurs non expliquée par le modèle PLS. Les observations avec des valeurs résiduelles X relativement importantes sont des valeurs aberrantes dans l'espace X, indiquant qu'elles ne sont pas expliquées correctement par le modèle.
Les valeurs résiduelles X sont le résultat de la différence entre les valeurs de prédicteur réelles et des valeurs calculées à partir des scores X ; leur échelle est identique à celle des prédicteurs d'origine. Semblable à la matrice X d'origine, la matrice des valeurs résiduelles X est une matrice n × p.
La matrice des valeurs résiduelles X est définie à l'origine sur la matrice X normalisée. Après avoir calculé la me composante et obtenu les vecteurs de scores X et de contributions X, Minitab calcule les valeurs résiduelles X.
Formule

Minitab calcule ensuite les valeurs résiduelles X non normalisées en multipliant les valeurs résiduelles X normalisées par l'écart type des valeurs de prédicteurs.
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| p | nombre de termes |
| i | observations de 1 à n |
| j | termes de 1 à p |
| t | scores X |
| l | contributions X |
Valeurs calculées X
Les valeurs calculées Y sont des combinaisons linéaires de scores X qui contiennent la variance des prédicteurs expliquée par le modèle PLS. Les observations avec des valeurs calculées X relativement faibles sont des valeurs aberrantes dans l'espace X et ne sont pas expliquées correctement par le modèle.
Semblable à la matrice X d'origine, la matrice des valeurs calculées X est une matrice n x p, dans laquelle n est le nombre d'observations et p le nombre de prédicteurs. Les valeurs calculées X se trouvent sur la même échelle que les prédicteurs.
La matrice des valeurs calculées X est initialisée sur la matrice zéro. Après avoir calculé la me composante et obtenu les vecteurs de scores X et de contributions X, Minitab calcule les valeurs calculées X. Si le nombre de composantes est égal à celui des prédicteurs, la valeur calculée X est égale à la valeur X d'origine.
Formule

Minitab calcule ensuite les valeurs calculées X non normalisées en multipliant les valeurs calculées X normalisées par l'écart type des valeurs de prédicteurs et en ajoutant la moyenne.
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| p | nombre de prédicteurs |
| i | nombre d'observations de 1 à n |
| j | nombre de prédicteurs de 1 à p |
| t | scores X |
| l | contributions X |
Scores Y
Les scores Y sont des combinaisons linéaires des variables de réponse. Les scores Y forment une matrice n ×m. Les scores Y sont des projections des observations des composantes PLS.
Formule
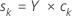
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| m | nombre de composantes |
| k | nombre de réponses de 1 à r |
| Y | matrice Y |
| c | contributions Y |
Contributions Y
Les contributions Y sont des coefficients linéaires liant les réponses aux scores Y. Les valeurs de contribution indiquent l'importance de la réponse correspondante pour la me composante. Les contributions Y forment une matrice r × m.
Formule

Notation
| Terme | Description |
|---|---|
| r | nombre de réponses |
| m | nombre de composantes |
| i | observations de 1 à n |
| k | réponses de 1 à r |
| Y | réponses |
| t | scores X |
Valeurs résiduelles Y
Les valeurs résiduelles Y sont des valeurs contenant la variance restante des réponses que n'explique pas le modèle PLS. Les observations avec des valeurs résiduelles Y relativement importantes sont des valeurs aberrantes dans l'espace Y ; elles ne sont donc pas expliquées correctement.
Les valeurs résiduelles Y sont le résultat de la différence des valeurs de réponse réelles et des valeurs calculées Y ; leur échelle est identique à celle des réponses d'origine. Semblable à la matrice Y d'origine, la matrice des valeurs résiduelles Y est une matrice n x r.
La matrice des valeurs résiduelles Y est définie à l'origine sur la matrice Y normalisée. Après avoir calculé la me composante et obtenu les vecteurs de scores X et de contributions Y, Minitab détermine les valeurs résiduelles Y normalisées.
Formule

Minitab calcule ensuite les valeurs résiduelles Y non normalisées en multipliant les valeurs résiduelles Y normalisées par l'écart type des valeurs de réponse correspondantes.
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| r | nombre de réponses |
| i | observations de 1 à n |
| k | réponses de 1 à r |
| t | scores X |
| c | contributions Y |
Valeurs calculées Y
Les valeurs calculées Y sont des combinaisons linéaires de scores X qui contiennent la variance des réponses expliquée par le modèle PLS. Les observations avec des valeurs calculées Y relativement faibles sont des valeurs aberrantes dans l'espace Y, et ne sont pas expliquées correctement.
Comme la matrice Y d'origine, la matrice des valeurs calculées Y est une matrice n x r. Elle est définie à l'origine sur la matrice zéro. Après avoir calculé la me composante et obtenu les vecteurs de scores X et de contributions Y, Minitab détermine les valeurs calculées Y normalisées.
Formule

Minitab calcule ensuite les valeurs calculées Y non normalisées en multipliant les valeurs calculées Y normalisées par l'écart type de la réponse correspondante et en ajoutant la moyenne.
Notation
| Terme | Description |
|---|---|
| n | nombre d'observations |
| r | nombre de réponses |
| i | observations de 1 à n |
| k | réponses de 1 à r |
| t | scores X |
| c | contributions Y |
