Sur ce thème
Etape 1 : Déterminer le nombre de composantes dans le modèle
L'objectif avec PLS est de sélectionner un modèle avec un nombre de composantes adapté et une bonne capacité de prévision. Lorsque vous ajustez un modèle PLS, vous pouvez réaliser une validation croisée pour déterminer le nombre optimal de composantes. Avec la validation croisée, Minitab sélectionne le modèle ayant le R2 prévu le plus élevé. Si vous n'utilisez pas la validation croisée, vous pouvez indiquer le nombre de composantes à inclure dans le modèle ou utiliser le nombre de composantes par défaut. Celui-ci est égal à 10 ou au nombre de prédicteurs dans vos données (le plus petit des deux). Etudiez le tableau des méthodes pour déterminer le nombre de composantes incluses dans le modèle par Minitab. Vous pouvez également examiner le diagramme de sélection de modèle.
Lorsque vous utilisez la méthode PLS, choisissez le modèle avec le plus petit nombre de composantes permettant d'expliquer une part suffisante de la variabilité des prédicteurs et des réponses. Pour déterminer le nombre de composantes le plus adapté pour vos données, examinez le tableau de sélection de modèle, notamment la variance X, le R2 et le R2 prévu. Le R2 prévu indique la capacité de prévision du modèle et n'est affiché que si vous effectuez une validation croisée.
Dans certains cas, vous pouvez utiliser un modèle différent de celui sélectionné par Minitab. Si vous avez utilisé la validation croisée, comparez le R2 et le R2 prévu. Par exemple, le fait de supprimer deux composantes du modèle ne diminue que légèrement le R2 prévu. Du fait que le R2 prévu n'a diminué que légèrement, le modèle n'est pas surajusté et vous pouvez décider qu'il convient mieux à vos données.
Une valeur de R2 prévu considérablement inférieure à R2 peut être un signe de surajustement du modèle. Un modèle est dit surajusté lorsqu'il inclut des termes ou des composantes pour des effets qui ne sont pas importants dans la population, bien qu'ils semblent importants dans les données échantillons. Le modèle est alors spécialement ajusté aux données des échantillons, mais risque ne pas être utile pour effectuer des prévisions concernant la population entière.
Si vous n'utilisez pas la validation croisée, vous pouvez examiner les valeurs de variance X dans le tableau de sélection de modèle pour déterminer la part de la variance de la réponse expliquée par chaque modèle.
Résultat principal : nombre de composantes
Dans ces résultats, la validation croisée a été utilisée dans le premier tableau de méthode et le modèle avec 4 composantes a été sélectionné. Dans le second tableau de méthode, la validation croisée n'a pas été utilisée. Minitab utilise le modèle avec 10 composantes (paramètre par défaut).
Sélection et validation de modèle pour Arôme
| Composantes | Variance X | Erreur | R carré | SomCar-ErrPrév | R carré (prév) |
|---|---|---|---|---|---|
| 1 | 0,158849 | 14,9389 | 0,637435 | 23,3439 | 0,433444 |
| 2 | 0,442267 | 12,2966 | 0,701564 | 21,0936 | 0,488060 |
| 3 | 0,522977 | 7,9761 | 0,806420 | 19,6136 | 0,523978 |
| 4 | 0,594546 | 6,6519 | 0,838559 | 18,1683 | 0,559056 |
| 5 | 5,8530 | 0,857948 | 19,2675 | 0,532379 | |
| 6 | 5,0123 | 0,878352 | 22,3739 | 0,456988 | |
| 7 | 4,3109 | 0,895374 | 24,0041 | 0,417421 | |
| 8 | 4,0866 | 0,900818 | 24,7736 | 0,398747 | |
| 9 | 3,5886 | 0,912904 | 24,9090 | 0,395460 | |
| 10 | 3,2750 | 0,920516 | 24,8293 | 0,397395 |
Résultat principal : variance X, R carré et R carré (prév)
Dans ces résultats, Minitab a sélectionné le modèle à 4 composantes qui a un R2 prévu d'environ 56 %. D'après la variance X, le modèle à 4 composantes explique presque 60 % de la variance des prédicteurs. Lorsque le nombre de composantes augmente, le R2 suit la même tendance, tandis que le R2 prévu diminue ; cela indique que les modèles avec plus de composantes sont susceptibles d'être surajustés.
Etape 2 : Déterminer si les données contiennent des valeurs aberrantes ou des points d'effet de levier
Pour déterminer si votre modèle est bien ajusté aux données, vous devez examiner les diagrammes à la recherche de valeurs aberrantes, de points d'effet de levier et d'autres schémas. Si vos données contiennent beaucoup de valeurs aberrantes ou de points d'effet de levier, le modèle ne fournit peut-être pas de prévisions valides.
- Valeurs aberrantes : observations comportant des valeurs résiduelles normalisées élevées, qui se trouvent hors des lignes de référence horizontales dans le diagramme.
- Points d'effet de levier : les observations avec des valeurs d'effet de levier ont des scores X éloignés de zéro et se situent à droite de la ligne de référence verticale.
Pour plus d'informations sur le diagramme des valeurs résiduelles en fonction de l'effet de levier, reportez-vous à la rubrique Graphiques pour la fonction Régression par les moindres carrés partiels.
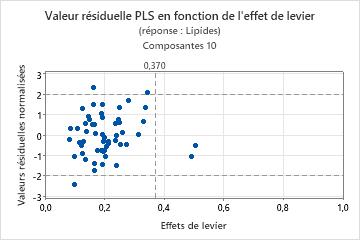
- Un motif non linéaire des points, ce qui indique que le modèle n'ajuste ou ne prévoit pas correctement les données.
- De grandes différences dans les valeurs ajustées et les valeurs à validation croisée, ce qui indique un point d'effet de levier (dans le cas d'une validation croisée).
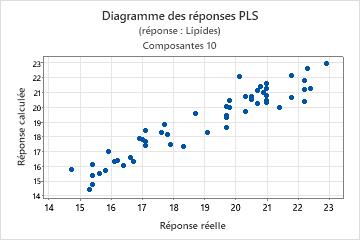
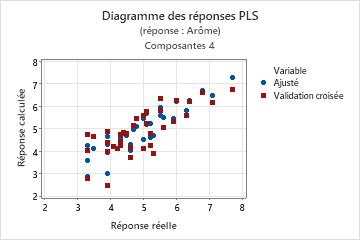
Etape 3 : Valider le modèle PLS avec un fichier de données de test
La régression PLS est souvent effectuée en deux étapes. La première étape, parfois appelée "entraînement", passe par le calcul d'un modèle de régression PLS pour un fichier de données échantillons (données d'entraînement). La seconde étape consiste à valider ce modèle avec un autre ensemble de données, souvent appelées "données de test". Pour valider le modèle avec le fichier de données de test, indiquez les colonnes des données de test dans la sous-boîte de dialogue Prévision. Minitab calcule de nouvelles valeurs de réponse pour chaque observation du fichier de données de test et compare la réponse prévue à la réponse réelle. En fonction de la comparaison, Minitab calcule le R2 de test, qui indique la capacité du modèle à prévoir de nouvelles réponses. Les valeurs de R 2 de test élevées indiquent que le modèle dispose d'une plus grande capacité de prévision.
Si vous utilisez la validation croisée, comparez le R2 au R2 carré prévu. Idéalement, ces valeurs doivent être similaires. Un R2 de test significativement inférieur au R2 prévu indique que la validation croisée est trop optimiste à propos de la capacité de prévision du modèle ou que les deux échantillons de données sont issus de populations différentes.
Si le fichier de données de test ne comprend pas de valeurs de réponse, Minitab ne calcule pas le R2 de test.
Réponse prévue pour les nouvelles observations avec le modèle pour Lipides
| Ligne | Valeur ajustée | ErT ajust | IC à 95 % | IP à 95 % |
|---|---|---|---|---|
| 1 | 18,7372 | 0,378459 | (17,9740; 19,5004) | (16,8612; 20,6132) |
| 2 | 15,3782 | 0,362762 | (14,6466; 16,1098) | (13,5149; 17,2415) |
| 3 | 20,7838 | 0,491134 | (19,7933; 21,7743) | (18,8044; 22,7632) |
| 4 | 14,3684 | 0,544761 | (13,2698; 15,4670) | (12,3328; 16,4040) |
| 5 | 16,6016 | 0,348485 | (15,8988; 17,3044) | (14,7494; 18,4538) |
| 6 | 20,7471 | 0,472648 | (19,7939; 21,7003) | (18,7861; 22,7080) |
Résultat principal : R 2 de test
Dans ces résultats, le R2 de test est d'environ 76 %. Le R2 prévu pour le fichier de données d'origine est d'environ 78 %. Vous pouvez en conclure que le modèle dispose d'une capacité de prévision adaptée étant donné que ces valeurs sont similaires.
