Valeurs ajustées
Les valeurs ajustées sont aussi appelées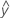 
. Les valeurs ajustées sont des estimations ponctuelles de la réponse moyenne pour certaines valeurs des prédicteurs. Les valeurs des prédicteurs sont également appelées valeurs X.
Interprétation
Les valeurs ajustées sont calculées en indiquant les valeurs de x correspondant à chaque observation de l'ensemble de données dans l'équation du modèle.
Par exemple, si l'équation est y = 5 + 10x, la valeur ajustée pour la valeur X (2) est 25 (25 = 5 + 10(2)).
ErT ajust
L'erreur type de l'ajustement (ErT ajust) estime la variation de la réponse moyenne estimée pour les valeurs de variables spécifiées. Le calcul de l'intervalle de confiance de la réponse moyenne utilise l'erreur type de la valeur ajustée. Les erreurs types ne sont jamais négatives.
Interprétation
Utilisez l'erreur type de l'ajustement pour mesurer la précision de l'estimation de la réponse moyenne. Plus l'erreur type est faible, plus la prévision de la réponse moyenne est précise. Par exemple, un analyste développe un modèle pour prévoir des délais de livraison. Pour un ensemble de paramètres de variables, le modèle prévoit un délai de livraison moyen de 3,80 jours. L'erreur type de l'ajustement pour ces paramètres est de 0,08 jours. Pour un deuxième ensemble de paramètres de variables, le modèle produit le même délai de livraison moyen avec une erreur type de l'ajustement de 0,02 jours. Avec le second ensemble de paramètres de variables, l'analyste peut affirmer avec plus de certitude que le délai de livraison moyen est proche de 3,80 jours.
Avec la valeur ajustée, l'erreur type de l'ajustement permet de créer un intervalle de confiance pour la réponse moyenne. Par exemple, selon le nombre de degrés de liberté, un intervalle de confiance à 95 % s'étend approximativement sur deux erreurs types au-dessus ou en dessous de la moyenne prévue. Dans l'exemple des délais de livraison, pour la réponse moyenne prévue de 3,80 jours lorsque l'erreur type est de 0,08, l'intervalle de confiance à 95 % est (3,64 ; 3,96) jours. Vous pouvez être certain à 95 % que la moyenne de la population se situe à l'intérieur de cette étendue. Lorsque l'erreur type est de 0,02, l'intervalle de confiance à 95 % est (3,76 ; 3,84) jours. L'intervalle de confiance pour le second ensemble de paramètres de variables est plus étroit, car l'erreur type est plus faible.
IC à 95 %
L'intervalle de confiance pour la valeur ajustée fournit une étendue de valeurs possibles pour la réponse moyenne en fonction des paramètres spécifiés pour les prédicteurs.
Interprétation
Utilisez l'intervalle de confiance afin d'évaluer l'estimation de la valeur ajustée pour les valeurs observées des variables.
Par exemple, avec un niveau de confiance de 95 %, vous pouvez être sûr à 95 % que l'intervalle de confiance comprend la moyenne de la population pour les valeurs indiquées des variables du modèle. L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Un grand intervalle de confiance traduit moins de certitude quant à la moyenne des futures valeurs. Si l'intervalle est trop grand pour être utile, envisagez d'augmenter l'effectif de l'échantillon.
IP de 95 %
L'intervalle de prévision est une étendue susceptible de contenir une seule réponse future pour une valeur de variable de prédiction.
Interprétation
Avec l'intervalle de prévision à 95 %, vous pouvez être sûr à 95 % que les nouvelles observations seront comprises dans l'intervalle. (Remarque : cela s'applique uniquement pour les valeurs incluses dans l'étendue des données lors de l'analyse.) L'intervalle est défini par une limite inférieure et une limite supérieure, calculées à partir du niveau de confiance et de l'erreur type de la prévision. L'intervalle de prévision est toujours plus large que l'intervalle de confiance du fait de l'incertitude supplémentaire de la prévision d'une seule réponse par rapport à une réponse moyenne.
R carré du test
Le R2 du test représente la proportion de variation dans les réponses expliquée par le modèle d'origine en utilisant les valeurs de prédicteurs des données de test.
Les données de test doivent comporter le même nombre de prédicteurs que les données d'origine. Le R2 du test ne peut être calculé que si les données de test comprennent des données de réponse pour chaque observation. Le R2 du test est calculé de la même manière que le R2.
Interprétation
Le R2 du test identifie la capacité du modèle de régression PLS à prévoir vos données de test. Plus les valeurs de R2 du test sont élevées, meilleures sont les capacités de prévision du modèle.
La régression PLS est souvent effectuée en deux étapes. La première étape, parfois appelée "entraînement", passe par le calcul d'un modèle de régression PLS pour un fichier de données échantillons (données d'entraînement). La seconde étape consiste à valider ce modèle avec un autre ensemble de données, souvent appelées "données de test". Certaines données de test comprennent des valeurs de réponse, d'autres n'en comportent pas. Si les données de test comprennent des valeurs de réponse, Minitab peut alors calculer un R2 du test.
Si vous utilisez la validation croisée, comparez le R2 au R2 carré prévu. Idéalement, ces valeurs doivent être similaires. Un R2 de test significativement inférieur au R2 prévu indique que la validation croisée est trop optimiste à propos de la capacité de prévision du modèle ou que les deux échantillons de données sont issus de populations différentes.
