Tableau de sélection et validation de modèle pour Régression par les moindres carrés partiels

Les composantes représentent le nombre de composantes incluses dans chaque modèle. Minitab affiche le modèle avec 1 composante, 2 composantes, etc. jusqu'à ce que le nombre de composantes spécifié soit atteint. Si vous n'avez indiqué aucun nombre de composantes à inclure dans le modèle, Minitab affiche les statistiques de sélection du modèle pour 10 composantes ou pour le nombre de prédicteurs, selon le moins élevé.

La variance X indique l'importance de la variance des termes expliquée par le modèle. La valeur de la variance X est comprise entre 0 et 1.

Plus la valeur de la variance X est proche de 1, mieux les composantes représentent l'ensemble de termes d'origine. S'il existe plusieurs réponses, la variance X est la même pour toutes.

L'erreur représente la somme des carrés de l'erreur, c'est-à-dire la somme des carrés des valeurs résiduelles. Elle quantifie la variation des données non expliquée par le modèle. Pour le modèle final, l'erreur correspond à la somme des carrés pour l'erreur résiduelle dans le tableau d'ANOVA.

R² représente le pourcentage de variation de la réponse expliqué par le modèle. Cette valeur est calculée comme 1 moins le rapport de la somme des carrés de l'erreur (variation non expliquée par le modèle) sur la somme totale des carrés (variation totale du modèle).

Interprétation

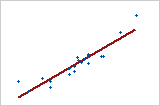
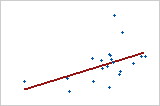
Utilisez la valeur R² pour déterminer l'ajustement du modèle à vos données. Plus la valeur R² est élevée, plus le modèle est ajusté à vos données. R² est toujours compris entre 0 et 100 %.

Vous pouvez utiliser une droite d'ajustement pour illustrer graphiquement différentes valeurs de R². La première droite représente un modèle de régression simple qui explique 85,5 % de la variation de la réponse. La deuxième représente un modèle qui explique 22,6 % de la variation de la réponse. Plus la proportion de la variation expliquée par le modèle de régression est importante, plus les points de données sont proches de la droite de régression ajustée. En théorie, si un modèle pouvait expliquer 100 % de la variation, les valeurs ajustées seraient toujours égales aux valeurs observées et, par conséquent, tous les points de données se situeraient sur la ligne de régression. Pourtant, même si la valeur R² est de 100 %, le modèle ne prévoit pas forcément bien les nouvelles observations.

Prenez en compte les problèmes suivants lors de l'interprétation de la valeur de R² :

• La valeur R² augmente toujours lorsque vous ajoutez des prédicteurs à un modèle. Par exemple, le meilleur modèle à 5 prédicteurs aura toujours une valeur R² au moins aussi élevée que celle du meilleur modèle à 4 prédicteurs. Par conséquent, R² est surtout utile pour comparer des modèles de même taille.

• Les petits échantillons ne fournissent pas d'estimation précise de la force de la relation entre la réponse et les prédicteurs. Par exemple, pour obtenir une valeur R² plus précise, vous devez utiliser un échantillon plus grand (en général, 40 ou plus).

• Les statistiques d'adéquation de l'ajustement ne sont qu'un des types de mesures permettant d'évaluer l'ajustement du modèle. Même si un modèle a une valeur souhaitable, vous devez consulter les graphiques des valeurs résiduelles pour vérifier que le modèle respecte les hypothèses.

Le R² prévu indique à quel point chaque modèle calculé prévoit la réponse ; il est uniquement calculé lorsque vous effectuez une validation croisée. Si les données contiennent une seule variable de réponse, Minitab sélectionne le modèle PLS ayant le R² prévu le plus élevé. Si les données contiennent plusieurs variables de réponse, Minitab sélectionne le modèle PLS ayant le R² prévu moyen le plus élevé pour toutes les variables de réponse. Le calcul du R² prévu s'effectue comme suit : suppression systématique de chaque observation de l'ensemble de données, estimation de l'équation de régression et évaluation de la capacité du modèle à prévoir l'observation supprimée. La valeur du R² prévu est comprise entre 0 et 100 %. Minitab affiche zéro lorsque les calculs de R² prévu génèrent des valeurs négatives.

La somme des carrés de l'erreur de prévision (SomCar-ErrPrév) permet de mesurer l'écart entre les valeurs ajustées et les valeurs observées. La SomCar-ErrPrév est semblable à la somme des carrés de l'erreur résiduelle (SCE), qui est la somme des carrés des valeurs résiduelles. Toutefois, la SomCar-ErrPrév utilise une autre méthode de calcul pour les valeurs résiduelles. La formule utilisée pour calculer la SomCar-ErrPrév revient à supprimer systématiquement chaque observation de l'ensemble de données, à estimer l'équation de régression et à évaluer la capacité du modèle à prévoir l'observation supprimée.