Sur ce thème
Diagramme de sélection des modèles
Le diagramme de sélection des modèles est un nuage de points des valeurs de R2 et de R2 prévu en tant que fonction du nombre de composantes ajustées ou à validation croisée. Il s'agit d'une représentation graphique du tableau de sélection et validation de modèle. Si vous n'optez pas pour la validation croisée, les valeurs de R2 prévu ne figurent pas dans votre diagramme. Minitab fournit un diagramme de sélection de modèle par réponse.
Interprétation
A l'aide de ce diagramme, comparez la puissance de modélisation et de prévision des différents modèles pour déterminer le nombre de composantes adapté à conserver dans votre modèle. La ligne verticale du diagramme indique le nombre de composantes que Minitab a sélectionnées pour le modèle PLS.
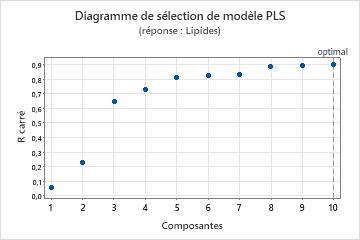
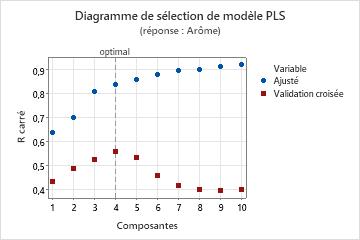
Diagramme des réponses
Le diagramme des réponses est un nuage de points des valeurs ajustées en fonction des réponses réelles. Si vous réalisez une validation croisée, le diagramme inclut également les valeurs ajustées en fonction des valeurs ajustées à validation croisée. Minitab propose un diagramme de réponses pour chaque réponse.
Interprétation
- Un motif non linéaire des points, ce qui indique que le modèle n'ajuste ou ne prévoit pas correctement les données.
- De grandes différences dans les valeurs ajustées et les valeurs à validation croisée, ce qui indique un point d'effet de levier (dans le cas d'une validation croisée).
Un modèle offrant une excellente capacité de prédiction a souvent une pente de 1 et coupe l'axe des Y à l'origine.
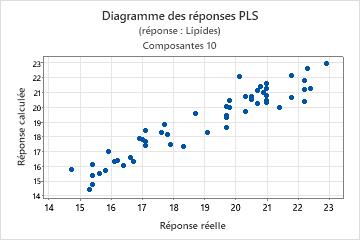
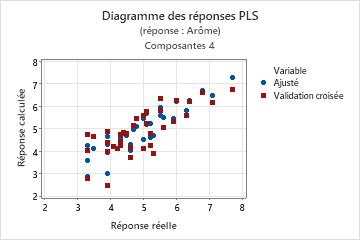
Diagramme des coefficients
Le diagramme des coefficients est un nuage de points projeté représentant les coefficients non normalisés de chaque prédicteur. Minitab propose un diagramme des coefficients pour chaque réponse.
Interprétation
Utilisez le diagramme des coefficients, ainsi que la sortie des coefficients de régression, pour comparer le signe et l'ampleur des coefficients de chaque prédicteur. Le diagramme facilite l'identification des prédicteurs selon leur importance dans le modèle.
Du fait que le diagramme n'affiche que des coefficients non normalisés, vous pouvez uniquement effectuer des comparaisons parmi l'ampleur des relations entre prédicteurs et réponse si les prédicteurs sont à la même échelle (des données spectrales, par exemple). Sinon, utilisez le diagramme des coefficients normalisés ou le diagramme de chargement pour comparer les pondérations des prédicteurs employés pour le calcul des composantes.
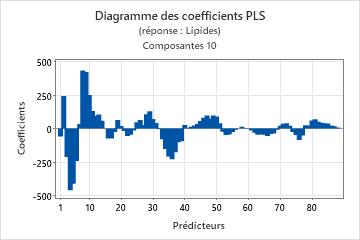
Diagramme des coefficients normalisés
Le diagramme des coefficients est un nuage de points projeté représentant les coefficients normalisés de chaque prédicteur. Minitab propose un diagramme des coefficients normalisés pour chaque réponse.
Interprétation
Utilisez ce diagramme ainsi que la sortie des coefficients de régression pour comparer le signe et l'ampleur des coefficients de chaque prédicteur. Le diagramme facilite l'identification des prédicteurs selon leur importance dans le modèle.
Du fait que le diagramme affiche des coefficients normalisés, vous pouvez effectuer des comparaisons parmi l'ampleur des relations entre les prédicteurs et la réponse même si les prédicteurs ne sont pas à la même échelle.
Si les prédicteurs sont à la même échelle, les schémas des coefficients des diagrammes normalisés et non normalisés présentent des similitudes. Il se peut que ces diagrammes ne paraissent pas identiques, cependant. En effet, les prédicteurs sont fortement corrélés, ce qui provoque de l'instabilité, et il existe des différences entre les écarts types des échantillons et les écarts types des populations.
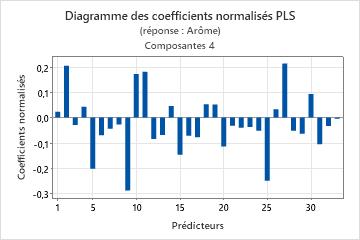
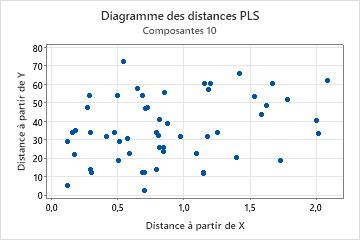
Diagramme des distances
Le diagramme des distances est un nuage de points de la distance entre le modèle X et le modèle Y de chaque observation. Distances de Y mesure à quel point une observation est ajustée dans l'espace y. Distances de X mesure à quel point une observation est ajustée dans l'espace x.
Interprétation
Lors de l'examen de ce diagramme, recherchez des points dont les distances sont supérieures aux autres points de l'axe des X ou de l'axe des Y. Les observations présentant des distances supérieures par rapport au modèle Y sont peut-être des valeurs aberrantes et les observations présentant des distances supérieures par rapport au modèle X sont peut-être des points d'effet de levier.
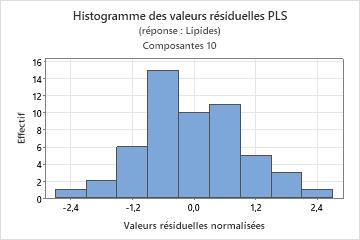
Histogramme des valeurs résiduelles
L'histogramme des valeurs résiduelles normalisées montre la distribution des valeurs résiduelles normalisées pour toutes les observations.
Interprétation
| Schéma | Ce que le schéma indique |
|---|---|
| Longue extrémité dans une direction | Asymétrie |
| Barre éloignée des autres | Une valeur aberrante |
Comme l'apparence de l'histogramme dépend du nombre d'intervalles utilisés pour regrouper les données, n'évaluez pas la normalité des valeurs résiduelles à l'aide d'un histogramme. Utilisez plutôt une droite de Henry. Les résultats de l'histogramme sont plus pertinents lorsque vous avez au moins 20 points de données. Si l'échantillon est trop petit, les barres de l'histogramme ne contiennent pas assez de points de données pour afficher l'asymétrie ou les valeurs aberrantes de manière fiable.
Droite de Henry des valeurs résiduelles
La droite de Henry des valeurs résiduelles affiche les valeurs résiduelles normalisées en fonction de leurs valeurs attendues lorsque la loi de distribution est normale.
Interprétation
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
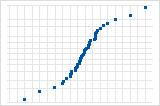
Une courbe S implique une distribution aux extrémités allongées.
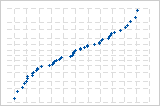
Une courbe S inversée implique une distribution aux extrémités écourtées.

Une courbe descendante implique une loi asymétrique à droite.

Quelques points situés loin de la ligne impliquent une distribution comportant des valeurs aberrantes.
Si vous observez une tendance non normale, utilisez les autres graphiques des valeurs résiduelles pour rechercher tout autre problème éventuel avec le modèle, tel que des termes manquants ou l'effet d'un ordre temporel. Si les valeurs résiduelles ne suivent pas une loi normale, les intervalles de confiance et les valeurs de p peuvent être inexacts.
Valeurs résiduelles en fonction des valeurs ajustées
Le diagramme des valeurs résiduelles en fonction des valeurs ajustées représente les valeurs résiduelles normalisées sur l'axe des Y et les valeurs ajustées sur l'axe des X.
Interprétation
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles suivent une loi normale et ont une variance constante. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Curviligne | Un terme d'ordre supérieur manquant |
| Un point très éloigné de zéro | Une valeur aberrante |
| Un point éloigné des autres points dans le sens des x | Un point influent |

Graphique avec valeur aberrante
Un des points a une valeur beaucoup élevée que tous les autres. Il s'agit donc d'une valeur aberrante. S'il existe un trop grand nombre de valeurs aberrantes, le modèle n'est peut-être pas acceptable. Vous devez essayer de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.
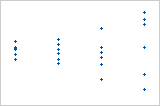
Graphique avec variance non constante
La variance des valeurs résiduelles augmente avec les valeurs ajustées. Plus les valeurs ajustées augmentent, plus les valeurs résiduelles sont dispersées. Ce schéma indique que les variances des valeurs résiduelles sont inégales (non constantes).
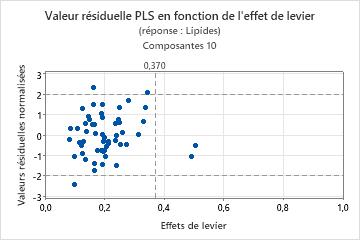
Valeurs résiduelles en fonction de l'effet de levier
Le diagramme des valeurs résiduelles en fonction de l'effet de levier est un nuage de points des valeurs résiduelles normalisées en fonction de l'effet de levier de chaque observation.
Interprétation
- Valeurs aberrantes : observations comportant des valeurs résiduelles normalisées supérieures à ± 2, qui se trouvent hors des lignes de référence horizontales dans le diagramme.
- Points à effet de levier : observations comportant des valeurs d'effet de levier supérieures à 2 m/n, m étant le nombre de composantes et n le nombre d'observations considérées comme extrêmes. Ces points ont des scores de x éloignés de zéro et se trouvent à droite de la ligne de référence verticale, qui est située au niveau la valeur 2 m/n sur l'axe des x. Si la valeur 2m/n est supérieure à 1, la ligne de référence ne figure pas dans le diagramme car les valeurs d'effet de levier sont toujours comprises entre 0 et 1.
Valeurs résiduelles en fonction de l'ordre
Le diagramme des valeurs résiduelles en fonction de l'ordre affiche les valeurs résiduelles normalisées dans l'ordre dans lequel elles ont été collectées.
Interprétation
Tendance
Equipe
Cycle
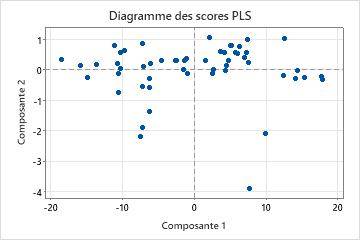
Diagramme des scores
Le diagramme des scores est un nuage de points des scores X tracé à partir des deux premières composantes du modèle.
Interprétation
Si les deux premières composantes expliquent en grande partie la variance des prédicteurs, la configuration des points de ce tracé reflète fidèlement la configuration multidimensionnelle d'origine de vos données. Pour vérifier à quel point le modèle explique la variance des prédicteurs, examinez les valeurs de variance X dans le tableau Sélection et validation de modèle. Si la valeur de variance X est élevée, le modèle explique une variance de signification des prédicteurs.
- Points d'effet de levier : les points qui sont éloignés de la plupart des points dans le graphique peuvent être des points d'effet de levier et avoir un effet significatif sur les résultats.
- Groupes : les regroupements de points peuvent indiquer au moins deux distributions de vos données, dont la description peut être améliorée dans certains modèles.
Remarque
Si votre modèle contient plus de 2 composantes, vous souhaiterez peut-être représenter les scores X des autres composantes à l'aide de la fonction Nuage de points. Pour cela, stockez la matrice de scores X, puis copiez-la en colonnes à l'aide de . Si votre modèle ne possède qu'une composante, ce graphique ne figure pas dans la sortie.
Diagramme des scores 3D
Le diagramme des scores 3D est un nuage de points tridimensionnel des scores X tracé à partir des trois premières composantes du modèle. Si les trois premières composantes illustrent en grande partie la variance des prédicteurs, la configuration des points de ce tracé reflète fidèlement la configuration multidimensionnelle d'origine de vos données. Pour vérifier à quel point le modèle explique la variance, examinez les valeurs de variance X dans le tableau Sélection et validation de modèle. Si la valeur de variance X est élevée, le modèle explique une variance de signification des prédicteurs.
Interprétation
- Points d'effet de levier : les points qui sont éloignés de la plupart des points dans le graphique peuvent être des points d'effet de levier et avoir un effet significatif sur les résultats.
- Groupes : les regroupements de points peuvent indiquer au moins deux distributions de vos données, dont la description peut être améliorée dans certains modèles.
Vous devez également utiliser les outils de graphiques 3D qui permettent de faire pivoter le graphique afin de l'afficher sous des perspectives différentes. Ces outils fournissant une image plus complète de vos données, vous pouvez identifier plus précisément les points d'effet de levier et les groupes de points.
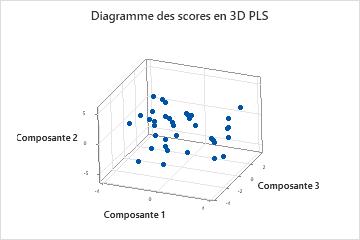
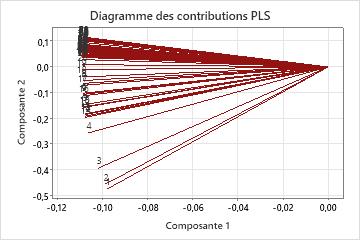
Diagramme des contributions
Le diagramme des contributions est un nuage de points des prédicteurs projeté sur les première et deuxième composantes du modèle. Il représente les contributions X de la seconde composante par rapport aux contributions X de la première. Chaque point, représentant un prédicteur, est connecté à (0,0) sur le graphique.
Interprétation
Le graphique de contribution illustre l'importance des prédicteurs par rapport aux deux premières composantes et s'avère particulièrement utile en cas de différence entre les échelles respectives des prédicteurs. Si les composantes expliquent en grande partie la variance X, représentée dans le tableau Sélection et validation de modèle, le graphique des contributions indique l'importance des prédicteurs dans l'espace X. Lorsque vous évaluez l'importance des prédicteurs dans l'ensemble du modèle, vous devez également mesurer l'incidence de la variance sur les composantes dans les réponses. Pour le vérifier, examinez les valeurs de R2 et de R2 prévu dans le tableau Sélection et validation de modèle.
- Les angles entre les lignes, représentant la corrélation entre les prédicteurs. Les angles plus petits qui correspondent aux prédicteurs à forte corrélation.
- Les prédicteurs avec les lignes plus longues, dont la première et la seconde composantes ont des contributions plus fortes et qui sont plus importants dans le modèle.
Remarque
Si votre modèle contient plus de 2 composantes, vous avez la possibilité de tracer les contributions X des autres composantes à l'aide de l'option Nuage de points. Pour cela, stockez la matrice de contributions X, puis copiez-la en colonnes à l'aide de .
Diagramme X des valeurs résiduelles
Le diagramme X des valeurs résiduelles est un graphique linéaire des valeurs résiduelles X en fonction des prédicteurs. Chaque ligne représente une observation et possède autant de points que de prédicteurs.
Interprétation
Le graphique matriciel diagonal des valeurs résiduelles X permet d'identifier les observations ou les prédicteurs que le modèle décrit mal. Ce graphique est particulièrement utile avec les prédicteurs de même échelle.
- Lorsque les lignes sont espacées sur le même point de l'axe des X, le modèle fournit une description incomplète du prédicteur à ce point.
- Lorsqu'une ligne du graphique dévie par rapport aux autres, le modèle décrit mal l'observation représentée par cette ligne.
Utilisez le graphique matriciel diagonal des valeurs résiduelles X pour étudier les schémas généraux des valeurs résiduelles et identifier les zones problématiques. Examinez ensuite les valeurs résiduelles X du résultat pour déterminer les observations et les prédicteurs que le modèle décrit mal.
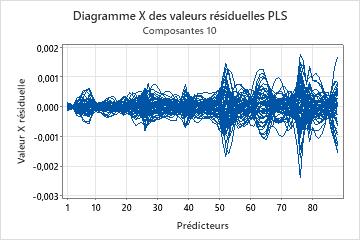
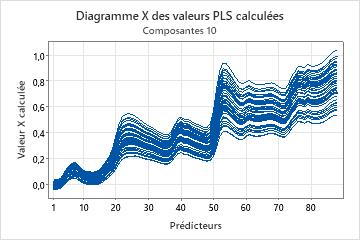
Diagramme X des valeurs calculées
Le diagramme X des valeurs calculées est un graphique linéaire des valeurs calculées X en fonction des prédicteurs. Chaque ligne représente une observation et possède autant de points que de prédicteurs.
Interprétation
Ce graphique permet d'identifier les observations ou les prédicteurs que le modèle décrit mal. Ce graphique est particulièrement utile avec les prédicteurs de même échelle.
Le diagramme X des valeurs calculées complète le diagramme des valeurs résiduelles X. Le cumul des deux graphiques produit un graphique des valeurs de prédicteur d'origine. Un prédicteur dont les valeurs calculées X fortement différentes des valeurs X d'origine n'est pas correctement décrit par le modèle.