Méthodes et formules pour la fonction Régression orthogonale

Le modèle d'erreur de mesure est le suivant :

Dans la régression orthogonale, la meilleure droite d'ajustement est celle qui minimise les distances orthogonales pondérées entre les points relevés et la droite. Si le rapport de variances d'erreur a pour valeur 1, les distances pondérées sont des distances euclidiennes.

Notation

Terme	Description
Yt	réponse observée
β0	ordonnée à l'origine
β1	pente
Xt	prédicteur observé
xt	valeur réelle et non observée de prédicteur
et, ut	erreurs de mesure ; et, ut sont indépendants avec une moyenne de 0 et des variances d'erreur de δe2 et δu2

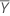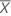Soit la moyenne d'échantillon (, ) et soit la matrice de covariance d'échantillon :

m_ZZ est une matrice 2X2 symétrique :

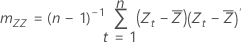
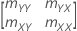
Notation

Terme	Description
Zt	(Yt, Xt)
n	effectif d'échantillon

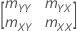
Si l'élément m_XY de la matrice de covariance d'échantillon n'est pas égal à 0 :

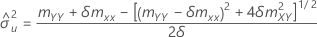
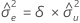
Si m_XY = 0 et m_YY < δm_XX,

Si m_XY = 0 et m_YY > δm_XX, les estimations des paramètres restants ne sont pas définies.

Notation

Terme	Description
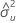	estimation de la variance de l'erreur pour X
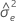	estimation de la variance de l'erreur pour Y
δ	rapport des variances d'erreur
mXY	élément de la matrice de covariance d'échantillon
mYY	élément de la matrice de covariance d'échantillon
mXX	élément de la matrice de covariance d'échantillon

Si l'élément m_XY de la matrice de covariance d'échantillon n'est pas égal à 0 :

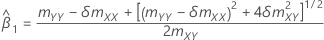
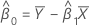
Si m_xy = 0 et m_yy < δm _xx','

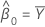
Si m_xy = 0 et m_yy > δm_xx, les estimations des paramètres restants ne sont pas définies.

Notation

Terme	Description
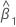	estimation de la pente
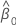	estimation de l'ordonnée à l'origine
mxy	élément de la matrice de covariance d'échantillon
myy	élément de la matrice de covariance d'échantillon
δ	rapport des variances d'erreur
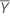	moyenne des valeurs de réponses
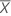	moyenne des valeurs des prédicteurs

Estimation de la matrice de covariance de la loi approximative pour l'ordonnée à l'origine et la pente :

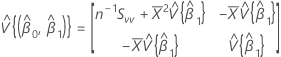
où :

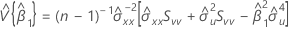
et

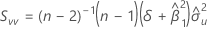
Si m_XY n'est pas égal à 0 :

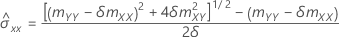
Si m_XY est égal à 0 et m_YY < δm_XX :

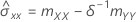
Notation

Terme	Description
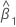	estimation de la pente
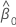	estimation de l'ordonnée à l'origine
mXY	élément de la matrice de covariance d'échantillon
mYY	élément de la matrice de covariance d'échantillon
mXX	élément de la matrice de covariance d'échantillon
δ	rapport des variances d'erreur
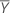	moyenne des valeurs de réponses
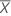	moyenne des valeurs des prédicteurs

L'intervalle de confiance 100(1 - α) % pour β₀ est le suivant :

où :

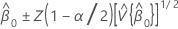
Z (1 - α / 2) est le 100 * (1 - α / 2) percentile pour la loi de distribution normale standard

et

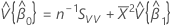, qui est un élément de la matrice de covariance de la loi approximative

Notation

Terme	Description
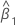	estimation de la pente
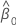	estimation de l'ordonnée à l'origine
α	qseuil de signification

L'intervalle de confiance 100(1 - α) % pour β₁ est le suivant :

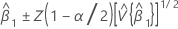
où :

Z(1 - α / 2) est le 100 * (1 - α / 2) percentile pour la loi de distribution normale standard

et

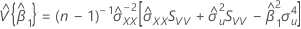
Notation

Terme	Description
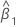	estimation de la pente
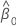	estimation de l'ordonnée à l'origine
α	seuil de signification

La valeur ajustée pour le prédicteur x dans la régression orthogonale est la suivante :

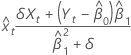
Notation

Terme	Description
δ	Rapport des variances d'erreur
Yt	te valeur de réponse
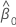	estimation de l'ordonnée à l'origine
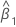	estimation de la pente

La valeur ajustée pour la réponse y dans la régression orthogonale est la suivante :

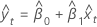
Notation

Terme	Description
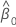	estimation de l'ordonnée à l'origine
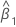	estimation de la pente
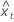	te valeur ajustée pour x

La valeur résiduelle d'une observation dans la régression orthogonale est :

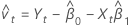
Notation

Terme	Description
Yt	te valeur de réponse
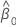	ordonnée à l'origine
Xt	te valeur de prédicteur
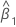	pente

La valeur résiduelle normalisée est utile pour l'identification des valeurs aberrantes. Elle est calculée comme suit :

où

Notation

Terme	Description
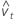	valeurs résiduelles
	écart type de la valeur résiduelle
δ	rapport des variances des erreurs
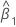	estimation de la pente
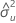	estimation de la variance de l'erreur pour X

Le prédicteur de Y_n + 1 est le suivant :

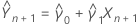
où :

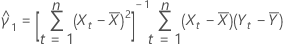
et

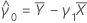
Notation

Terme	Description
Xt	te valeur de prédicteur
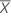	moyenne des valeurs des prédicteurs
Yt	te valeur de réponse
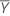	moyenne des valeurs de réponses

où :

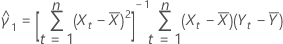
Notation

Terme	Description
myy	variance de l'échantillon pour Y
mxy	covariance d'échantillon entre les variables aléatoires X et Y