Interprétation des résultats principaux pour la fonction Régression orthogonale

Suivez les étapes ci-dessous pour interpréter une analyse de régression orthogonale. Les résultats principaux incluent les intervalles de confiance pour les coefficients, la droite d'ajustement et les graphiques des valeurs résiduelles.

Sur ce thème

Etape 1 : Déterminer si les mesures de deux instruments ou méthodes diffèrent
Etape 2 : Déterminer si la droite de régression est ajustée à vos données

Etape 1 : Déterminer si les mesures de deux instruments ou méthodes diffèrent

La régression orthogonale est souvent utilisée en chimie clinique ou en laboratoire pour déterminer si deux instruments ou méthodes fournissent des mesures comparables. Si l'intervalle de confiance pour le terme constant contient la valeur zéro et si l'intervalle pour le terme linéaire contient la valeur 1, vous pouvez généralement en conclure que les mesures obtenues avec les deux instruments sont comparables.

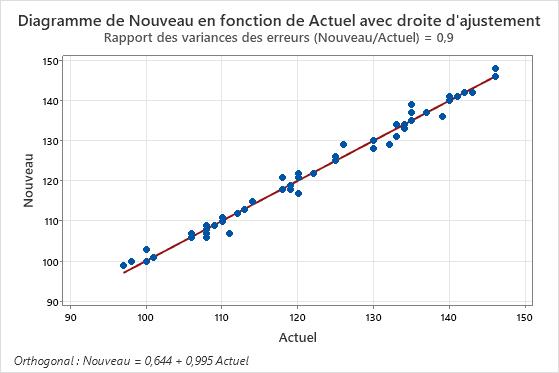
Vous devez également examiner le diagramme avec la droite d'ajustement pour déterminer le degré d'ajustement du modèle aux données.

Rapport des variances des erreurs (Nouveau/Actuel) : 0,9

Equation de régression
Nouveau = 0,644 + 0,995 Actuel

Coefficients

Prédicteur	Coeff	Coef ErT	Z	P	IC 95 % approx.
Constante	0,64441	1,74470	0,3694	0,712	(-2,77513; 4,06395)
Actuel	0,99542	0,01415	70,3461	0,000	(0,96769; 1,02315)

Variances d'erreur

Variable	Variance
Nouveau	1,07856
Actuel	1,19840

Résultat principal : IC 95 % approx.

Dans ces résultats, l'intervalle de confiance pour le terme constant est à environ (−3, 4). Etant donné que l'intervalle contient 0, cette partie de l'analyse ne prouve pas que les mesures des deux instruments diffèrent.

L'intervalle de confiance pour le terme linéaire est à environ (0,97, 1,02). Etant donné que l'intervalle contient 1, cette partie de l'analyse ne prouve pas que les mesures des deux instruments diffèrent.

Aucun des intervalles ne prouvant que les mesures des deux instruments diffèrent, vous pouvez généralement en conclure que les mesures sont comparables. Vous devez également vérifier que le modèle s'ajuste correctement aux données en examinant le diagramme avec la droite d'ajustement et les graphiques des valeurs résiduelles.

Etape 2 : Déterminer si la droite de régression est ajustée à vos données

Utilisez le diagramme et la droite d'ajustement pour déterminer si l'équation de régression orthogonale est adaptée aux données. Lorsque le modèle s'ajuste aux données, les points sont proches de la droite de régression. Vous pouvez notamment examiner la droite d'ajustement avec les critères suivants :

L'échantillon contient un nombre adapté d'observations dans l'étendue des valeurs de prédicteurs.
L'échantillon ne présente pas de courbure non ajustée au modèle.
L'échantillon ne comporte pas de valeurs aberrantes, ce qui peut fortement influer sur les résultats. Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de saisie de données ou les erreurs de mesure visibles. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.

Ce diagramme illustre des mesures réalisées à l'aide de deux instruments ou méthodes comparables. Les points suivent la droite d'ajustement avec un éclatement minimal et sans schéma traduisant des différences systématiques entre les méthodes.

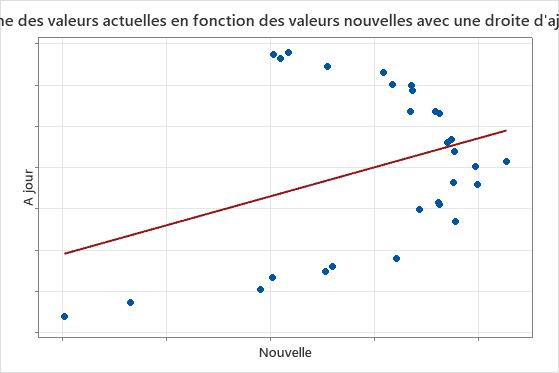
Dans les résultats ci-après, les intervalles de confiance pour les coefficients ne prouvent pas que les mesures des deux instruments diffèrent. Cependant, le diagramme présente des points éloignés de la droite, indiquant que les mesures des deux instruments ne sont pas comparables. Les données n'étant pas ajustées à l'équation, la conclusion générale est que les instruments diffèrent.

Coefficients

Prédicteur	Coeff	Coef ErT	Z	P	IC 95 % approx.
Constante	-0,00000	0,215424	-0,0000	1,000	(-0,422224; 0,42222)
Nouveau	1,00000	0,517586	1,9320	0,053	(-0,014450; 2,01445)