Sur ce thème
Diagramme avec droite d'ajustement
Le diagramme avec droite d'ajustement montre les données de réponses et de prédicteurs. Il inclut une droite de régression orthogonale qui représente l'équation de régression orthogonale.
A des fins de comparaison, vous pouvez afficher la droite d'ajustement des moindres carrés. Les différences importantes entre les deux droites indiquent dans quelle mesure les résultats dépendent de la prise en compte de l'incertitude dans les valeurs des variables de prévision. Les valeurs des moindres carrés sont égales aux valeurs prévues pour la régression orthogonale ; vous pouvez donc également utiliser la droite des moindres carrés pour étudier les valeurs prévues.
Interprétation
- L'échantillon contient un nombre adapté d'observations dans l'étendue des valeurs de prédicteurs.
- L'échantillon ne présente pas de courbure non ajustée au modèle.
- L'échantillon ne comporte pas de valeurs aberrantes, ce qui peut fortement influer sur les résultats. Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de saisie de données ou les erreurs de mesure visibles. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.
Vous utilisez souvent la régression orthogonale en chimie clinique ou en technique de laboratoire pour déterminer si deux instruments ou méthodes fournissent des mesures comparables.
Ce diagramme illustre des mesures réalisées à l'aide de deux instruments ou méthodes comparables. Les points suivent la droite d'ajustement avec un éclatement minimal et sans schéma traduisant des différences systématiques entre les méthodes.
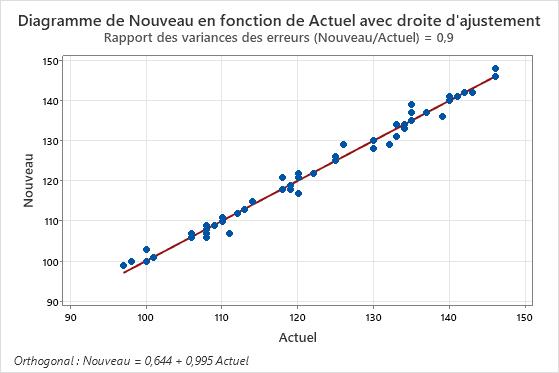
Dans les résultats ci-après, les intervalles de confiance pour les coefficients ne prouvent pas que les mesures des deux instruments diffèrent. Cependant, le diagramme présente des points éloignés de la droite, indiquant que les mesures des deux instruments ne sont pas comparables. Les données n'étant pas ajustées à l'équation, la conclusion générale est que les instruments diffèrent.
Coefficients
| Prédicteur | Coeff | Coef ErT | Z | P | IC 95 % approx. |
|---|---|---|---|---|---|
| Constante | -0,00000 | 0,215424 | -0,0000 | 1,000 | (-0,422224; 0,42222) |
| Nouveau | 1,00000 | 0,517586 | 1,9320 | 0,053 | (-0,014450; 2,01445) |
Histogramme des valeurs résiduelles
L'histogramme des valeurs résiduelles montre la distribution des valeurs résiduelles pour toutes les observations.
Interprétation
| Schéma | Ce que le schéma indique |
|---|---|
| Longue extrémité dans une direction | Asymétrie |
| Barre éloignée des autres | Une valeur aberrante |
Vous utilisez souvent la régression orthogonale en chimie clinique ou en technique de laboratoire pour déterminer si deux instruments ou méthodes mesurent la même chose. Lorsque le modèle ne satisfait pas les hypothèses, cela peut s'expliquer par le fait que les méthodes ne mesurent pas la même chose.
Comme l'apparence de l'histogramme dépend du nombre d'intervalles utilisés pour regrouper les données, n'évaluez pas la normalité des valeurs résiduelles à l'aide d'un histogramme. Utilisez plutôt une droite de Henry.
Les résultats de l'histogramme sont plus pertinents lorsque vous avez au moins 20 points de données. Si l'échantillon est trop petit, les barres de l'histogramme ne contiennent pas assez de points de données pour afficher l'asymétrie ou les valeurs aberrantes de manière fiable.
Droite de Henry des valeurs résiduelles
La droite de Henry des valeurs résiduelles affiche les valeurs résiduelles en fonction de leurs valeurs attendues lorsque la loi de distribution est normale.
Interprétation
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
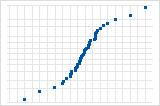
Une courbe S implique une distribution aux extrémités allongées.
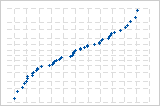
Une courbe S inversée implique une distribution aux extrémités écourtées.

Une courbe descendante implique une loi asymétrique à droite.

Quelques points situés loin de la ligne impliquent une distribution comportant des valeurs aberrantes.
Vous utilisez souvent la régression orthogonale en chimie clinique ou en technique de laboratoire pour déterminer si deux instruments ou méthodes mesurent la même chose. Si vous constatez un schéma non normal, cela peut s'expliquer par le fait que les méthodes ne mesurent pas la même chose. Examinez également les autres graphiques des valeurs résiduelles pour détecter tout autre problème relatif au modèle, comme l'effet d'un ordre temporel. Si les valeurs résiduelles ne suivent pas une loi normale, les intervalles de confiance et les valeurs de p peuvent être inexacts.
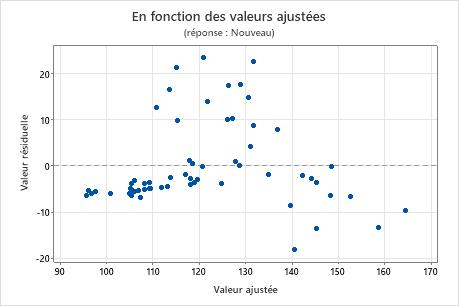
Valeurs résiduelles en fonction des valeurs ajustées
Le graphique des valeurs résiduelles en fonction des valeurs ajustées représente les valeurs résiduelles sur l'axe des Y et les valeurs ajustées pour le prédicteur sur l'axe des X.
Vous utilisez souvent la régression orthogonale en chimie clinique ou en technique de laboratoire pour déterminer si deux instruments ou méthodes mesurent la même chose. Lorsque le modèle ne satisfait pas les hypothèses, cela peut s'expliquer par le fait que les méthodes ne mesurent pas la même chose.
Interprétation
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles suivent une loi normale et ont une variance constante. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Curviligne | Un terme d'ordre supérieur manquant |
| Un point très éloigné de zéro | Une valeur aberrante |
| Un point éloigné des autres points dans le sens des x | Un point influent |

Graphique avec valeur aberrante
Un des points a une valeur beaucoup élevée que tous les autres. Il s'agit donc d'une valeur aberrante. S'il existe un trop grand nombre de valeurs aberrantes, le modèle n'est peut-être pas acceptable. Vous devez essayer de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.
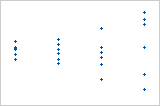
Graphique avec variance non constante
La variance des valeurs résiduelles augmente avec les valeurs ajustées. Plus les valeurs ajustées augmentent, plus les valeurs résiduelles sont dispersées. Ce schéma indique que les variances des valeurs résiduelles sont inégales (non constantes).
Valeurs résiduelles en fonction de l'ordre
Le diagramme des valeurs résiduelles en fonction de l'ordre affiche les valeurs résiduelles dans l'ordre dans lequel les données ont été collectées.
Interprétation
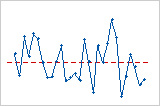
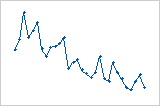
Tendance
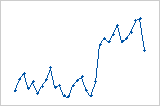
Equipe
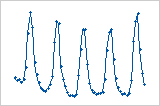
Cycle
Valeurs résiduelles en fonction des variables
Le diagramme des valeurs résiduelles en fonction des variables affiche les valeurs résiduelles en fonction d'une autre variable. La variable peut déjà être présente dans votre modèle. Il se peut aussi que la variable ne soit pas dans le modèle, mais que vous la soupçonniez d'avoir un effet sur la réponse.
Interprétation
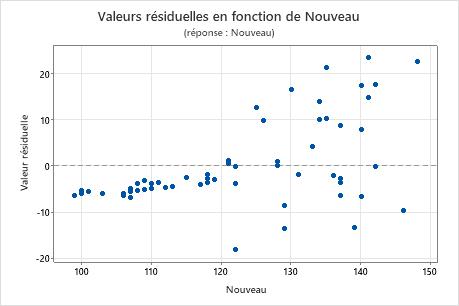
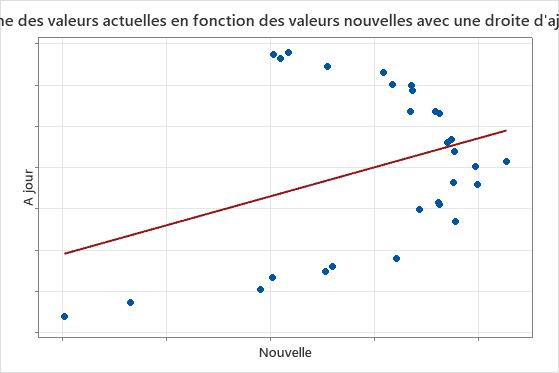
Vous utilisez souvent la régression orthogonale en chimie clinique ou en technique de laboratoire pour déterminer si deux instruments ou méthodes mesurent la même chose. Les schémas révélés dans un graphique des valeurs résiduelles en fonction de la variable de réponse ou de la variable de prévision peuvent expliquer en quoi une méthode est différente d'une autre.
Dans ces résultats, le graphique des valeurs résiduelles en fonction des valeurs ajustées présente un schéma où toutes les valeurs résiduelles élevées apparaissent au centre. Un graphique des valeurs résiduelles en fonction de la variable de réponse montre que plus les relevés de la nouvelle méthode sont élevés, plus la concordance avec l'autre analyse se détériore.